Сортировка методом пузырька в python

Программа упорядочения строк в алфавитном порядке[править]

#include<stdlib.h>
#include<string.h>
#include<stdio.h>
#define N 100
#define M 30
intmain(intargc,char*argv[]){
charaN];
intn,i;
scanf("%d",&n);
for(i=;i<n;i++)
scanf("%s",&ai]);
qsort(a,n,sizeof(charM]),(int(*)(constvoid*,constvoid*))strcmp);
for(i=;i<n;i++)
printf("%s\n",ai]);
return;
}

Обратите внимание на сложное приведение типов.

Функция strcmp, объявленная в файле string.h имеет следующий прототип:

int strcmp(const char*, const char*);

То есть функция получает два аргумента — указатели на кусочки памяти, где хранятся элементы типа char,
то есть два массива символов, которые не могут быть изменены внутри функции strcmp (запрет на изменение задается с помощью модификатора const).

В то же время в качестве четвертого элемента функция qsort хотела бы иметь функцию типа

int cmp(const void*, const void*);

В языке Си можно осуществлять приведение типов являющихся типами функции. В данном примере тип

int (*)(const char*, const char*); // функция, получающая два элемента типа 'const char *' и возвращающая элемент типа 'int' 

приводится к типу

int (*)(const void*, const void*); // функция, получающая два элемента типа 'const void *' и возвращающая элемент типа 'int'

Варианты алгоритма

Сорт коктейлей

Производной пузырьковой сортировки является сортировка коктейлей или шейкерная сортировка. Этот метод сортировки основан на следующем наблюдении: при пузырьковой сортировке элементы могут быстро перемещаться в конец массива, но перемещаются в начало массива только по одной позиции за раз.

Идея сортировки коктейлей состоит в чередовании направления маршрута. Получается несколько более быстрая сортировка, с одной стороны, потому что она требует меньшего количества сравнений, с другой стороны, потому что она перечитывает самые последние данные при изменении направления (поэтому они все еще находятся в кэш-памяти ). Однако количество обменов, которые необходимо произвести, идентично (см. Выше). Таким образом, время выполнения всегда пропорционально n 2 и, следовательно, посредственно.

Три прыжка вниз

Код для этой сортировки очень похож на пузырьковую сортировку. Подобно пузырьковой сортировке, при этой сортировке первыми отображаются самые крупные элементы. Однако это не работает с соседними элементами; он сравнивает каждый элемент массива с тем, который находится на месте большего, и обменивается, когда находит новый, больший.

tri_jump_down(Tableau T)
   pour i allant de taille de T - 1 à 1
       pour j allant de 0 à i - 1
           si T < T
               échanger(T, T)

Сортировка combsort

Вариант пузырьковой сортировки, называемый гребенчатой ​​сортировкой ( combsort ), был разработан в 1980 году Влодзимежем Добосевичем и вновь появился в апреле 1991 года в журнале Byte Magazine . Он исправляет главный недостаток пузырьковой сортировки, которой являются «черепахи», и делает алгоритм столь же эффективным, как и быстрая сортировка .

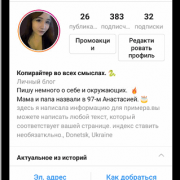
Сортировка пузырьком Python

# Python реализация сортировки пузырьком

def bubbleSort(arr):

n = len(arr)

# Проход через все элементы массива

for i in range(n):

# Последние i элементы уже на месте

for j in range(0, n-i-1):

# проход массива от 0 до n-i-1

# Поменять местами, если найденный элемент больше

# чем следующий элемент

if arr > arr :

arr, arr = arr, arr

# Код тестирования

arr = 

bubbleSort(arr)

print ("Сортированный массив:")

for i in range(len(arr)):

print ("%d" %arr),

Результат:

Сортированный массив:

11 12 22 25 34 64 90

Оптимизированная реализация

Приведенная выше сортировка методом пузырька всегда выполняется, даже если массив отсортирован. Ее можно оптимизировать путем остановки алгоритма, применяемой в том случае, если внутренний цикл не произвел никакой замены.

С/С++

// Оптимизированная реализация пузырьковой сортировки

#include <stdio.h>

void swap(int *xp, int *yp)

{

int temp = *xp;

*xp = *yp;

*yp = temp;

}

// Оптимизированная версия пузырьковой сортировки

void bubbleSort(int arr[], int n)

{

int i, j;

bool swapped;

for (i = 0; i < n-1; i++)

{

swapped = false;

for (j = 0; j < n-i-1; j++)

{

if (arr > arr)

{

swap(&arr, &arr);

swapped = true;

}

}

// Если в процессе прохода не было ни одной замены, то выход из функции

if (swapped == false)

break;

}

}

/* Функция вывода массива */

void printArray(int arr[], int size)

{

int i;

for (i=0; i < size; i++)

printf("%d ", arr);

printf("n");

}

// Программа тестирования функций, приведенных выше

int main()

{

int arr[] = {64, 34, 25, 12, 22, 11, 90};

int n = sizeof(arr)/sizeof(arr);

bubbleSort(arr, n);

printf("Сортированный массив: n");

printArray(arr, n);

return 0;

}

Метод «пузырька»[править]

Один из простейших алгоритмов решения — метод «пузырька».

#include<stdio.h>
intmain(){
intn,i,j;
scanf_s("%d",&n);
intan];
// считываем количество чисел n

// формируем массив n чисел
for(i=;i<n;i++){
scanf_s("%d",&ai]);
}
for(i=;i<n-1;i++){
// сравниваем два соседних элемента.
for(j=;j<n-i-1;j++){
if(aj>aj+1]){
// если они идут в неправильном порядке, то  
//  меняем их местами. 
inttmp=aj];
aj=aj+1;
aj+1=tmp;
}
}
}
}

Понятно, что после первого «пробега» самый большой элемент массива окажется на последнем месте.
После второго пробега мы будем уверены, что второй по величине элемент
находится на предпоследнем месте.

Задача: Докажите, что достаточно n−1{\displaystyle n-1} пробега, чтобы элементы массива упорядочились.

Решив эту задачу, вы докажете, что метод «пузырька» решает задачу сортировки.

Пузырьковая сортировка и её улучшения

Сортировка пузырьком

Сортировка пузырьком — один из самых известных алгоритмов сортировки. Здесь нужно последовательно сравнивать значения соседних элементов и менять числа местами, если предыдущее оказывается больше последующего. Таким образом элементы с большими значениями оказываются в конце списка, а с меньшими остаются в начале.

Этот алгоритм считается учебным и почти не применяется на практике из-за низкой эффективности: он медленно работает на тестах, в которых маленькие элементы (их называют «черепахами») стоят в конце массива. Однако на нём основаны многие другие методы, например, шейкерная сортировка и сортировка расчёской.

 void BubbleSort(vector<int>& values) {
  for (size_t idx_i = 0; idx_i + 1 < values.size(); ++idx_i) {
    for (size_t idx_j = 0; idx_j + 1 < values.size() - idx_i; ++idx_j) {
      if (values < values) {
        swap(values, values);
      }
    }
  }
}

 

Сортировка перемешиванием (шейкерная сортировка)

Шейкерная сортировка отличается от пузырьковой тем, что она двунаправленная: алгоритм перемещается не строго слева направо, а сначала слева направо, затем справа налево.

 void ShakerSort(vector<int>& values) {
  if (values.empty()) {
    return;
  }
  int left = 0;
  int right = values.size() - 1;
  while (left <= right) {
    for (int i = right; i > left; --i) {
      if (values > values) {
        swap(values, values);
      }
    }
    ++left;
    for (int i = left; i < right; ++i) {
      if (values > values) {
        swap(values, values);
      }
    }
    --right;
  }
} 

Сортировка расчёской

Сортировка расчёской — улучшение сортировки пузырьком. Её идея состоит в том, чтобы «устранить» элементы с небольшими значения в конце массива, которые замедляют работу алгоритма. Если при пузырьковой и шейкерной сортировках при переборе массива сравниваются соседние элементы, то при «расчёсывании» сначала берётся достаточно большое расстояние между сравниваемыми значениями, а потом оно сужается вплоть до минимального.

Первоначальный разрыв нужно выбирать не случайным образом, а с учётом специальной величины — фактора уменьшения, оптимальное значение которого равно 1,247. Сначала расстояние между элементами будет равняться размеру массива, поделённому на 1,247; на каждом последующем шаге расстояние будет снова делиться на фактор уменьшения — и так до окончания работы алгоритма.

 void CombSort(vector<int>& values) {
  const double factor = 1.247; // Фактор уменьшения
  double step = values.size() - 1;

  while (step >= 1) {
    for (int i = 0; i + step < values.size(); ++i) {
      if (values > values) {
        swap(values, values);
      }
    }
    step /= factor;
  }
  // сортировка пузырьком
  for (size_t idx_i = 0; idx_i + 1 < values.size(); ++idx_i) {
    for (size_t idx_j = 0; idx_j + 1 < values.size() - idx_i; ++idx_j) {
      if (values < values) {
        swap(values, values);
      }
    }
  }
}
 

Подробный разбор пузырьковой сортировки

Давайте разберем подробно как работает пузырьковая сортировка

Первая итереация (первый повтор алгоритма) меняет между собой 4 и 2 так как цифра два меньше чем четыре 2<4, повторюсь что алгоритм меняет значения между собой если, слева оно меньше чем справа. Далее происходит сверка между 4 и 3, и так как 3 меньше чем 4 (3<4) происходит обмен значениями. Потом проходит проверку между 4 и 8 и так как значение 4 меньше чем 8 то не происходит обмена, ведь уже и так всё на своих местах.

Далее сравнивается 8 и 1 и так как 1 меньше чем 8 (1<8) и оно не находиться слева то происходит обмен значениями.После это первый повтор алгоритма заканчивается, на анимации я выделил это зеленым фоном.

В итоге по окончанию работы алгоритма пузырьковой сортировки мы имеем следующий порядок числового массива: 2 3 4 1 8

и начинается второй повтор алгоритма.

Далее сравнивается 2 и 3 и так как два меньше чем три и оно находиться слева то просто идем дальше ничего не трогая. Также проверяем и 3 и 4 и тоже самое условие выполняется 3<4 и оно слева. Дальше проверяется 4 и 1 и тут мы видим что число 1<4 и не находиться слева, поэтому алгоритм меняет их местами. В крайний раз для второго повторения алгоритма проверяется 4 и 8, но тут всё в порядке, и мы дошли до конца начинаем третье повторение. Итоги для второго повторения такие : 2 3 1 4 8

Третье повторение пузырькового алгоритма начинается с сравнения 2 и 3, тут алгоритм проверяет что 2<3 и 2 находиться слева и оставляет их в покое и идет дальше. Сравнение же 3 и 1 показывает что 1 то меньше чем три, но почему то не слева и меняет их местами. Далее идет сравнение 3 и 4, тут всё в порядке и так далее до сравнения 4 и 8.

После этого получается следующий результат: 2 1 3 4 8

Как мы видим почти все цифры уже на своих местах и в порядке возрастания! Осталось только в последнем повторении пузырькового алгоритма поменять местами 2 и 1 и всё. После того как алгоритм закончил свою работу и проверил что цифры больше нельзя поменять местами он перестает работать с таким вот результатом: 1 2 3 4 8

Сортировка пузырьком

Этот метод, вероятно, является первым достаточно сложным модулем, который должен написать любой начинающий программист. Это очень простая конструкция, которая знакомит учащихся с основами работы алгоритмов.

Пузырьковая (обменная) использует двумерный или одномерный массив и механизм обмена. Большинство языков программирования имеют встроенную функцию для перестановки элементов. Даже если функция обмена не существует, требуется всего пара дополнительных строк кода. Вместо перебора массива, пузырьковая работает по схеме сравнения соседних пар объектов. Шаги:

1. Если элементы расположены не в правильном порядке, они меняются местами так, что самый большой из двух перемещается вверх. Этот процесс продолжается до тех пор, пока самый большой из объектов, не окажется на первом месте.
2. После этого начинается поиск следующего по величине элемента.
3. Перестановка остановится, когда весь массив окажется в правильном порядке.

Сортировка пузырьком на Pascal (Паскаль):

Сортировка массива методом пузырька на Python (Питон):

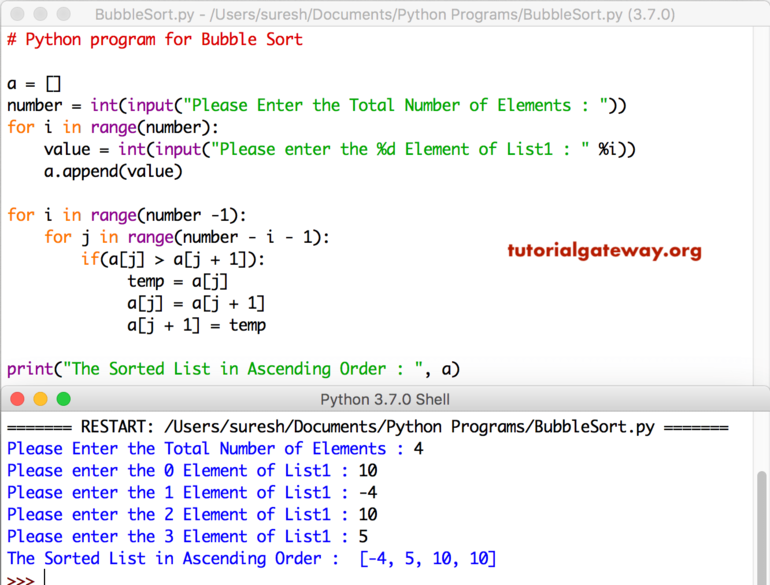
На Java:

Из-за своей простоты этот метод часто используется для представления концепции алгоритма сортировки. В компьютерной графике она популярна благодаря своей способности выявлять очень маленькую ошибку (например, перестановку всего двух элементов) в почти отсортированных массивах и исправлять ее с помощью линейной сложности.

Какой способ обработки данных выбрать, специалист решает сам, в зависимости от времени и объема информации.

Простые сортировки

Сортировка вставками

При сортировке вставками массив постепенно перебирается слева направо. При этом каждый последующий элемент размещается так, чтобы он оказался между ближайшими элементами с минимальным и максимальным значением.

 void InsertionSort(vector<int>& values) {
  for (size_t i = 1; i < values.size(); ++i) {
    int x = values;
    size_t j = i;
    while (j > 0 && values > x) {
      values = values;
      --j;
    }
    values = x;
  }
}

 

Сортировка выбором

Сначала нужно рассмотреть подмножество массива и найти в нём максимум (или минимум). Затем выбранное значение меняют местами со значением первого неотсортированного элемента. Этот шаг нужно повторять до тех пор, пока в массиве не закончатся неотсортированные подмассивы.

 void SelectionSort(vector<int>& values) {
  for (auto i = values.begin(); i != values.end(); ++i) {
    auto j = std::min_element(i, values.end());
    swap(*i, *j);
  }
}
 

Эффективные сортировки

Быстрая сортировка

Этот алгоритм состоит из трёх шагов. Сначала из массива нужно выбрать один элемент — его обычно называют опорным. Затем другие элементы в массиве перераспределяют так, чтобы элементы меньше опорного оказались до него, а большие или равные — после. А дальше рекурсивно применяют первые два шага к подмассивам справа и слева от опорного значения.

Быструю сортировку изобрели в 1960 году для машинного перевода: тогда словари хранились на магнитных лентах, а сортировка слов обрабатываемого текста позволяла получить переводы за один прогон ленты, без перемотки назад.

 int Partition(vector<int>& values, int l, int r) {
  int x = values;
  int less = l;

  for (int i = l; i < r; ++i) {
    if (values <= x) {
      swap(values, values);
      ++less;
    }
  }
  swap(values, values);
  return less;
}

void QuickSortImpl(vector<int>& values, int l, int r) {
  if (l < r) {
    int q = Partition(values, l, r);
    QuickSortImpl(values, l, q - 1);
    QuickSortImpl(values, q + 1, r);
  }
}

void QuickSort(vector<int>& values) {
  if (!values.empty()) {
    QuickSortImpl(values, 0, values.size() - 1);
  }
}
 

Сортировка слиянием

Сортировка слиянием пригодится для таких структур данных, в которых доступ к элементам осуществляется последовательно (например, для потоков). Здесь массив разбивается на две примерно равные части и каждая из них сортируется по отдельности. Затем два отсортированных подмассива сливаются в один.

 void MergeSortImpl(vector<int>& values, vector<int>& buffer, int l, int r) {
  if (l < r) {
    int m = (l + r) / 2;
    MergeSortImpl(values, buffer, l, m);
    MergeSortImpl(values, buffer, m + 1, r);

    int k = l;
    for (int i = l, j = m + 1; i <= m || j <= r; ) {
      if (j > r || (i <= m && values < values)) {
        buffer = values;
        ++i;
      } else {
        buffer = values;
        ++j;
      }
      ++k;
    }
    for (int i = l; i <= r; ++i) {
      values = buffer;
    }
  }
}

void MergeSort(vector<int>& values) {
  if (!values.empty()) {
    vector<int> buffer(values.size());
    MergeSortImpl(values, buffer, 0, values.size() - 1);
  }
}
 

Пирамидальная сортировка

При этой сортировке сначала строится пирамида из элементов исходного массива. Пирамида (или двоичная куча) — это способ представления элементов, при котором от каждого узла может отходить не больше двух ответвлений. А значение в родительском узле должно быть больше значений в его двух дочерних узлах.

Пирамидальная сортировка похожа на сортировку выбором, где мы сначала ищем максимальный элемент, а затем помещаем его в конец. Дальше нужно рекурсивно повторять ту же операцию для оставшихся элементов.

 void HeapSort(vector<int>& values) {
std::make_heap(values.begin(), values.end());
for (auto i = values.end(); i != values.begin(); --i) {
std::pop_heap(values.begin(), i);
 }
}
 

Ещё больше интересного — в соцсетях Академии

Базовый алгоритм

Принцип и псевдокод

Алгоритм просматривает массив и сравнивает последовательные элементы. Когда два последовательных элемента вышли из строя, они меняются местами .

После первого полного обхода таблицы самый большой элемент обязательно находится в конце таблицы, в ее конечной позиции. Действительно, как только самый большой элемент встречается во время курса, он плохо сортируется по отношению ко всем следующим элементам, поэтому меняются каждый раз до конца курса.

После первого запуска, когда самый большой элемент находится в своей конечной позиции, его больше не нужно обрабатывать. Однако остальная часть таблицы все еще в беспорядке. Поэтому необходимо пройти его заново, остановившись на предпоследнем элементе. После этого второго прогона два самых больших элемента занимают окончательное положение. Поэтому необходимо повторять траектории таблицы, пока два самых маленьких элемента не будут помещены в свое окончательное положение.

Следующий псевдокод взят из Knuth .

tri_à_bulles(Tableau T)
   pour i allant de (taille de T)-1 à 1
       pour j allant de 0 à i-1
           si T < T
               (T, T) = (T, T)

Текущая оптимизация этой сортировки заключается в ее прерывании, как только путь элементов, возможно, все еще находящихся в беспорядке (внутренний цикл), выполняется без обмена. Фактически это означает, что отсортирован весь массив. Эта оптимизация требует дополнительной переменной.

tri_à_bulles_optimisé(Tableau T)
    pour i allant de (taille de T)-1 à 1
        tableau_trié := vrai
        pour j allant de 0 à i-1
            si T < T
                (T, T) = (T, T)
                tableau_trié := faux
        si tableau_trié
            fin tri_à_bulles_optimisé

Сложность

Для неоптимизированной сортировки, то временная сложность составляет Θ ( п 2 ), с п размера массива.

Для оптимизированной сортировки количество итераций внешнего цикла составляет от 1 до n . Действительно, мы можем показать, что после i -го шага последние i элементов массива находятся на своих местах. На каждой итерации выполняется ровно n -1 сравнений и не более n -1 обменов.

• Наихудший случай ( n итераций) достигается, когда наименьший элемент находится в конце массива. Тогда сложность равна Θ ( n 2 ).
• В среднем сложность также Θ ( n 2 ). Действительно, количество обменов пар последовательных элементов равно количеству инверсий перестановки , то есть пар ( i , j ) таких, что i < j и T ( i )> T ( j ). Этот номер не зависит от способа организации обмена. Когда начальный порядок элементов массива случайный, он в среднем равен n ( n -1) / 4.
• Наилучший случай (единичная итерация) достигается, когда массив уже отсортирован. В этом случае сложность линейная.

Пошаговый пример

Применение пузырьковой сортировки к таблице чисел «5 1 4 2 8»; для каждого шага сравниваемые элементы выделены жирным шрифтом.

Шаг 1.

1.1. ( 5 1 4 2 8) ( 1 5 4 2 8). Числа 5 и 1 сравниваются, и, как и 5> 1, алгоритм меняет их местами. 1.2. (1 5 4 2 8) (1 4 5 2 8). Обмен, потому что 5> 4. 1.3. (1 4 5 2 8) (1 4 2 5 8). Обмен, потому что 5> 2. 1.4. (1 4 2 5 8 ) (1 4 2 5 8 ). Нет обмена, потому что 5 <8. В конце этого шага число находится на своем последнем месте, самом большом: 8.→{\ displaystyle \ to} →{\ displaystyle \ to} →{\ displaystyle \ to} →{\ displaystyle \ to}

2-й шаг.

2.1. ( 1 4 2 5 8) ( 1 4 2 5 8). Без изменений. 2.2. (1 4 2 5 8) (1 2 4 5 8). Обмен. 2.3. (1 2 4 5 8) (1 2 4 5 8). Без изменений. 5 и 8 не сравниваются, так как мы знаем, что 8 уже на своем последнем месте. Случайно все числа уже отсортированы, но это еще не обнаружено алгоритмом.→{\ displaystyle \ to} →{\ displaystyle \ to} →{\ displaystyle \ to}

Шаг 3.

3.1. ( 1 2 4 5 8) ( 1 2 4 5 8). Без изменений. 3.2. (1 2 4 5 8) (1 2 4 5 8). Без изменений. Последние два числа исключаются из сравнений, так как мы знаем, что они уже на своем последнем месте. Поскольку на этом шаге 3 обмена не было, оптимизированная сортировка завершается.→{\ displaystyle \ to} →{\ displaystyle \ to}

Шаг 4.

4.1. ( 1 2 4 5 8) ( 1 2 4 5 8). Без изменений. Сортировка завершена, потому что мы знаем, что 4 наибольших числа, а следовательно, и 5- е , находятся на своем последнем месте.→{\ displaystyle \ to}

Использовать

Пузырьковая сортировка. Список был построен в декартовой системе координат, где каждая точка ( x , y ) указывает, что значение y хранится в индексе x . Затем список будет отсортирован пузырьковой сортировкой по значению каждого пикселя

Обратите внимание, что сначала сортируется самый большой конец, а меньшим элементам требуется больше времени, чтобы переместиться в правильное положение.

Хотя пузырьковая сортировка является одним из простейших алгоритмов сортировки для понимания и реализации, ее сложность O ( n 2 ) означает, что ее эффективность резко снижается в списках из более чем небольшого числа элементов. Даже среди простых алгоритмов сортировки O ( n 2 ) такие алгоритмы, как сортировка вставкой , обычно значительно более эффективны.

Из-за своей простоты пузырьковая сортировка часто используется для ознакомления с концепцией алгоритма или алгоритма сортировки для начинающих студентов- информатиков . Тем не менее, некоторые исследователи, такие как Оуэн Астрахан , пошли на многое, чтобы осудить пузырьковую сортировку и ее неизменную популярность в образовании по информатике, рекомендуя даже не преподавать ее.

Жаргон Файл , который лихо звонков bogosort «архетипический извращенно ужасный алгоритм», также вызывает пузырьковую сортировку «общий плохой алгоритм». Дональд Кнут в своей книге «Искусство компьютерного программирования» пришел к выводу, что «пузырьковой сортировке, похоже, нечего рекомендовать, кроме броского названия и того факта, что она приводит к некоторым интересным теоретическим проблемам», некоторые из которых он затем обсуждает.

Пузырьковая сортировка асимптотически эквивалентна по времени работы сортировке вставкой в ​​худшем случае, но эти два алгоритма сильно различаются по количеству необходимых перестановок. Экспериментальные результаты, такие как результаты Astrachan, также показали, что сортировка вставкой работает значительно лучше даже в случайных списках. По этим причинам многие современные учебники алгоритмов избегают использования алгоритма пузырьковой сортировки в пользу сортировки вставкой.

Пузырьковая сортировка также плохо взаимодействует с современным аппаратным обеспечением ЦП. Он производит как минимум вдвое больше записей, чем сортировка вставкой, вдвое больше промахов в кеш и асимптотически больше ошибочных прогнозов переходов . Эксперименты с сортировкой строк Astrachan в Java показывают, что пузырьковая сортировка примерно в пять раз быстрее сортировки вставкой и на 70% быстрее сортировки по выбору .

В компьютерной графике пузырьковая сортировка популярна благодаря своей способности обнаруживать очень маленькие ошибки (например, перестановку всего двух элементов) в почти отсортированных массивах и исправлять их с линейной сложностью (2 n ). Например, он используется в алгоритме заполнения многоугольника, где ограничивающие линии сортируются по их координате x в определенной строке сканирования (линия, параллельная оси x ), а с увеличением y их порядок изменяется (два элемента меняются местами) только при пересечения двух линий. Пузырьковая сортировка — это стабильный алгоритм сортировки, как и сортировка вставкой.

Анализ

Пример пузырьковой сортировки. Начиная с начала списка, сравните каждую соседнюю пару, поменяйте их местами, если они не в правильном порядке (последняя меньше первой). После каждой итерации необходимо сравнивать на один элемент меньше (последний), пока не останется больше элементов для сравнения.

Представление

Пузырьковая сортировка имеет наихудший случай и среднюю сложность О ( n 2 ), где n — количество сортируемых элементов. Большинство практических алгоритмов сортировки имеют существенно лучшую сложность в худшем случае или в среднем, часто O ( n  log  n ). Даже другое О ( п 2 ) алгоритмы сортировки, такие как вставки рода , как правило , не работать быстрее , чем пузырьковой сортировки, а не более сложным. Следовательно, пузырьковая сортировка не является практическим алгоритмом сортировки.

Единственное существенное преимущество пузырьковой сортировки перед большинством других алгоритмов, даже быстрой сортировкой , но не сортировкой вставкой , заключается в том, что в алгоритм встроена способность определять, что список сортируется эффективно. Когда список уже отсортирован (в лучшем случае), сложность пузырьковой сортировки составляет всего O ( n ). Напротив, большинство других алгоритмов, даже с лучшей средней сложностью , выполняют весь процесс сортировки на множестве и, следовательно, являются более сложными. Однако сортировка вставкой не только разделяет это преимущество, но также лучше работает со списком, который существенно отсортирован (имеет небольшое количество инверсий ). Кроме того, если такое поведение желательно, его можно тривиально добавить к любому другому алгоритму, проверив список перед запуском алгоритма.

Кролики и черепахи

Расстояние и направление, в котором элементы должны перемещаться во время сортировки, определяют производительность пузырьковой сортировки, поскольку элементы перемещаются в разных направлениях с разной скоростью. Элемент, который должен двигаться к концу списка, может перемещаться быстро, потому что он может принимать участие в последовательных заменах. Например, самый большой элемент в списке будет выигрывать при каждом обмене, поэтому он перемещается в свою отсортированную позицию на первом проходе, даже если он начинается рядом с началом. С другой стороны, элемент, который должен двигаться к началу списка, не может двигаться быстрее, чем один шаг за проход, поэтому элементы перемещаются к началу очень медленно. Если наименьший элемент находится в конце списка, потребуется n −1 проход, чтобы переместить его в начало. Это привело к тому, что эти типы элементов были названы кроликами и черепахами соответственно в честь персонажей басни Эзопа о Черепахе и Зайце .

Были предприняты различные попытки уничтожить черепах, чтобы повысить скорость сортировки пузырей. Сортировка коктейлей — это двунаправленная сортировка пузырьков, которая идет от начала до конца, а затем меняет свое направление, идя от конца к началу. Он может довольно хорошо перемещать черепах, но сохраняет сложность наихудшего случая O (n 2 ) . Сортировка гребенкой сравнивает элементы, разделенные большими промежутками, и может очень быстро перемещать черепах, прежде чем переходить к все меньшим и меньшим промежуткам, чтобы сгладить список. Его средняя скорость сопоставима с более быстрыми алгоритмами вроде быстрой сортировки .

Пошаговый пример

Возьмите массив чисел «5 1 4 2 8» и отсортируйте его от наименьшего числа к наибольшему числу, используя пузырьковую сортировку. На каждом этапе сравниваются элементы, выделенные жирным шрифтом . Потребуется три прохода;

Первый проход

( 5 1 4 2 8) → ( 1 5 4 2 8). Здесь алгоритм сравнивает первые два элемента и меняет местами, поскольку 5> 1.

(1 5 4 2 8) → (1 4 5 2 8), поменять местами, поскольку 5> 4

(1 4 5 2 8) → (1 4 2 5 8), поменять местами, поскольку 5> 2

(1 4 2 5 8 ) → (1 4 2 5 8 ). Теперь, поскольку эти элементы уже упорядочены (8> 5), алгоритм не меняет их местами.

Второй проход

( 1 4 2 5 8) → ( 1 4 2 5 8)

(1 4 2 5 8) → (1 2 4 5 8), поменять местами, поскольку 4> 2

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Теперь массив уже отсортирован, но алгоритм не знает, завершился ли он. Алгоритму требуется один дополнительный полный проход без какой-либо подкачки, чтобы знать, что он отсортирован.

Третий проход

( 1 2 4 5 8) → ( 1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8) → (1 2 4 5 8)

(1 2 4 5 8 ) → (1 2 4 5 8 )

Программа

Программа, в которой сначала необходимо ввести размер одномерного массива, после чего массив заполняется случайными числами и сортируется методом пузырька
// bu_sort.cpp: определяет точку входа для консольного приложения.

 1 #include "stdafx.h"
 2 #include <iostream>
 3 using std::cout;
 4 using std::cin;
 5 using std::endl;
 6  
 7 const int n = 100;
 8  
 9 void Swap(int &x,int &y)
10 {
11 	x = x + y;
12 	y = x - y;
13 	x = x - y;
14 }
15  
16 void Bubble_Sort(int *a, int LeanghtArray)
17 {
18 	for (int i = 1; i < LeanghtArray-1; ++i){
19 		for (int i2 = 1; i2 < LeanghtArray-1; ++i2){
20 			if (ai2 > ai2+1]){ 
21 				Swap(ai2], ai2+1]);
22 			}
23 		}
24 	}
25 }
26  
27  
28 int _tmain(int argc, _TCHAR* argv[])
29 {
30 	int an], a1n], i, i2;
31 	for (int i = 1; i < n; i++){ ai = rand(); a1i = ai]; }
32 	
33 	Bubble_Sort(a, n);
34 	
35 	for (int i = 1; i < n; i++){ cout << ai <<" "<<a1i<<endl; }
36 	cin >> i;
37 	return ;
38 }

[Рекурсия] Рекурсивное написание пузырьковой сортировки

http-equiv=»Content-Type» content=»text/html;charset=UTF-8″>style=»clear:both;»>

Предисловие: Как по прихоти написать рекурсию пузырьковой сортировки? ? Затем я проверил Baidu и обнаружил, что многие методы записи являются рекурсивными, например цикл for внутри рекурсии. Есть ли чистая рекурсия для полной пузырьковой сортировки?

Первая пузырьковая сортировка показана на рисунке выше. Порядок сравнения: 01 12 23 34.

Второй раз 01 12 23

Третий раз 01 12

Четвертый раз 01

После этих конечных сравнений элементы массива упорядочиваются.

Написание и понимание рекурсии в основном одинаковы. Первая нерекурсивная базовая пузырьковая сортировка, порядок сортировки — это убывающая упорядоченная последовательность n — количество элементов

Сортировку пузырьков можно анализировать следующим образом: i начинается с 1, а сортировка заканчивается, когда она накапливается до значения, большего или равного n. Каждый i будет сопровождаться обработкой пузырьков n-i. Каждый процесс барботирования j сопровождается дополнительной операцией обмена. к

Тогда рекурсивный выход i> = n

Тогда условие для изменения i, j: j> = n-i

Затем вы можете завершить рекурсивную запись:

Вы можете исправить любые ошибки. Вчера бессонница без причины Что случилось? ?

Интеллектуальная рекомендация

Пожалуйста, реализуйте функцию для преобразованияЗаменить каждый пробел»% 20″. Например, когда строка We We Happy. Строка после замены — We% 20Are% 20Happy. Встроенные функции для строк Pyth…

EventHub :: MeetEvents Method, Mneedtscandevices Переменная процесса вызова подробный анализ         …         if (mNeedToScanDevices…

Просто поймите:   1. Типы элементов в списке могут быть разными, он поддерживает числа, строки и даже списки (так называемая вложенность). 2. Список представляет собой список элементов, заключенн…

Главная идея: ответ: Этот вопрос найти несложно, f указывает, что состояние выбранной точки равно i, это минимальная стоимость, а dis указывает количество сокровищ от начальной точки до i. , а…

Отскок летающей овцы Однажды Лостмонки изобрел сверхэластичное устройство и, чтобы похвастаться перед своими друзьями-овцами, пригласил маленькую овечку поиграть в игру. В начале игры Lostmonkey разме…

Вам также может понравиться

Инструменты: Android Studio activity_main.xml fragment_1.xml fragment_1.java fragment_2.xml fragment_2.java fragment_3.xml fragment_3.java MainActivity.java Эффект интерфейса…

50% людей знают, как использовать Word, чтобы получать платежные ведомости, но только 10% знают, как сделать так, чтобы платежные ведомости Word были строго отформатированы, а сотрудники, которые экон…

Используйте poi для импорта Excel и инкапсуляции его в JavaBean По причинам спроса я недавно сделал импорт в Excel и упаковал его в JavaBean, чтобы реализовать функцию пакетного импорта. И добиться со…

Смени тему На этой картинке изображен темный кимби (кажется, именно кимби создал этот вид) Официальные ярлыки…

 …