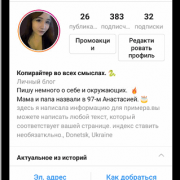
Округл (round) округление значений в excel

Правила округления десятичной дроби

Десятичную дробь можно округлить:

• до целого числа с точностью до единиц, десятков, сотен и т.д.;
• до определенного разряда дробной части: десятых, сотых, тысячных, десятитысячных и т.д.

Но, прежде чем перейти к правилам округления, давайте еще раз вспомним, из чего состоит десятичная дробь. В качестве примера – от тысяч до десятитысячных:

Округление дробной части

Итак, чтобы выполнить округление десятичной дроби, придерживаемся следующего плана действий:

1. Отмечаем разряд, до которого следует округлить дробь. Его можно отделить от следом идущих цифр разделительной линией.
2. Далее возможно два варианта (согласно правилам округления чисел):
   • если после выбранного разряда идут цифры , 1, 2, 3 или 4, то цифру этого разряда мы оставляем той же, а все остальные цифры после линии убираем.
   • если после выбранного разряда стоят цифры 5, 6, 7, 8 или 9, то к цифре этого разряда прибавляем единицу и, как в пункте выше, все цифры с правой стороны от линии убираем.

Пример 1: округлим 12,624 до десятых.

Пример 2: округлим 5,176 до сотых.

Если десятичную дробь требуется округлить до целого числа (до единиц), смотрим на цифру, которая идет сразу же после запятой (разряд – десятые). Если это 5, 6, 7, 8 или 9, то к единицам в целой части прибавляем число 1, а всю дробную часть отбрасываем. В остальных случаях просто убираем дробную часть без каких-либо изменений целой части.

Примеры округления десятичных дробей до целого числа:

• 2,15 ≈ 2;
• 4,64 ≈ 5;
• 7,063 ≈ 7;
• 12,814 ≈ 13.

Примечание: Если дробь требуется округлить до целого числа большего разряда, чем единицы (десятки, сотни, тысячи и т.д.), отбрасываем дробную часть, затем округляем полученный результат согласно правилам округления натуральных чисел.

Пример 1: выполним округление до десятков числа 156,71:

Пример 2: выполним округление до сотен числа 8134,145:

Особый случай: последняя цифра – ноль

Если в результате округления десятичной дроби последней цифрой в дробной части остается , его нельзя убирать. Это нужно для того, чтобы наглядно было понято, до какого разряда было выполнено округление.

Примеры округления с нулем на конце

• 5,01 ≈ 5,0 (до десятых);
• 3,199 ≈ 3,20 (до сотых).

Остановимся подробнее на втором примере. Т.к. в следующем разряде после сотых стоит цифра 9, значит по правилам округления к сотым мы прибавляем единицу: 9 + 1 = 10. Следовательно, в разряде сотых мы пишем ноль, а единицу прибавляем к десятым (1 + 1 = 2).

ОКРУГЛТ

Довольно полезная функция ОКРУГЛТ. С ее помощью можно добиться округления не только до нужного разряда (слева или справа от запятой), но и вообще до нужной точности (кратности). К примеру, нужно рассчитать заказ изделий в штуках, но так, чтобы он был равен целому количеству ящиков. Если в ящике 6 шт, то заказываемое количество должно быть кратно шести. Или другой пример. Нужно, чтобы расчетная цена заканчивалась либо на 00, либо на 50, то есть имела кратность 50 рублей. Функция ОКРУГЛТ легко решает такие задачи.

Очень, очень правильная функция. Позволяет избежать 3-х промежуточных расчетов (разделить на кратность, округлить до целого и снова умножить на кратность, как я сам делал, пока не узнал про эту формулу).

Изменение количества отображаемых знаков после запятой без изменения числового значения

Выполнение такого рода действия осуществляется при помощи настроек числового формата, путем уменьшения количества знаков после запятой, при этом само числовое значение не округляется, округляется только его отображение на экране монитора. Внести изменения в настройки числового формата, можно при помощи кнопок «Увеличить разрядность» и «Уменьшить разрядность» на ленте Excel 2007 во вкладке «Главная», в группе «Число».

В других версиях Excel эти кнопки выглядят аналогично. Изменения в настройки числового формата, а именно увеличение либо уменьшение количества отображаемых знаков после запятой, можно внести в настройках формата ячеек. Не буду повторять о том, как вызвать окно «Формат ячеек»
разными способами, так как ранее этот вопрос уже рассматривался. Использование вышеописанного метода округления может приводить к некоторым нежелательным последствиям, например вот к такому:

Как видно из примера, некорректная настройка числового формата привела к тому, что 2+3=6, что неверно.

Неявная типизация

Чтобы указать призвольный тип переменных, можно использовать неявную типизацию. Для этого используется ключевое слово .

Пример:

var hello = "Привет, мир!";
var c = 20;
             
Console.WriteLine(c.GetType().ToString());
Console.WriteLine(hello.GetType().ToString());

Var используется вместо названия типа данных. Присвоенное значение позволяет компилятору выводить тип данных. В примере ; определяет тип переменной . Целочисленные значения по умолчанию рассматриваются как ,  поэтому переменная имеет тип .

Но такие переменные имеют свои ограничения:

1Нельзя определить неявную переменную и сразу ее инициализировать.

// верно
int a;
a = 20;
 
// неверно
var c;
c = 20;

2Неявная переменная не может иметь значение , в этом случае компилятор не определит автоматически тип данных.

// неверно
var c=null;

Точные правила округления чисел

При округлении десятичных дробей недостаточно просто отбросить цифры после округляемого разряда. Убедиться в этом можно на таком примере. Если в магазине куплено 2 кг 150 г конфет, то говорят, что приобретено около 2 кг сладостей. Если же вес составляет 2 кг 850 г, то производят округление в большую сторону, то есть около 3 кг. То есть видно, что иногда округляемый разряд изменен. Когда и как это проделывают, смогут ответить точные правила:

1. Если после округляемого разряда следует цифра 0, 1, 2, 3 или 4, то округляемый оставляют неизменным, а все последующие цифры отбрасываются.
2. Если после округляемого разряда следует цифра 5, 6, 7, 8 или 9, то округляемый увеличивают на единицу, а все последующие цифры также отбрасываются.

К примеру, как правильно дробь 7,41 приблизить к единицам. Определяют цифру, которая следует за разрядом. В данном случае это 4. Следовательно, согласно правилу, число 7 оставляют неизменным, а цифры 4 и 1 отбрасывают. То есть получаем 7.

Если округляется дробь 7,62, то после единиц следует цифра 6. Согласно правилу, 7 необходимо увеличить на 1, а цифры 6 и 2 отбросить. То есть в результате получится 8.

Представленные примеры показывают, как округлить десятичные дроби до единиц.

Приближение до целых

Отмечено, что округлять до единиц можно точно так же, как и до целых. Принцип один и тот же. Остановимся подробнее на округлении десятичных дробей до определенного разряда в целой части дроби. Представим пример приближения 756,247 до десятков. В разряде десятых располагается цифра 5. После округляемого разряда следует цифра 6. Следовательно, по правилам необходимо выполнить следующие шаги:

• округление в большую сторону десятков на единицу,
• в разряде единиц цифру 6 заменяют нулем,
• цифры в дробной части числа отбрасываются,
• в результате получают 760.

Обратим внимание на некоторые значения, в которых процесс математического округления до целых по правилам не отображает объективную картину. Если взять дробь 8,499, то, преобразовывая его по правилу, получаем 8

Но по сути это не совсем так. Если поразрядно округлить до целых, то вначале получим 8,5, а затем отбрасываем 5 после запятой, и осуществляем округление в большую сторону.

Получаем 9, что, в принципе, не сосем точно. То есть в таких значениях погрешность существенна. Поэтому оцениваем задачу и, если ситуация позволяет, то лучше использовать значение 8,5.

Приближение до десятых

Как округлить до десятых, до сотых, до тысячных? Операция осуществляется по таким же правилам, как и до целых. Основная задача – правильно определить округляемый разряд и знак, который следует за ним.

К примеру, дробь 6,7864 при доведении:

• до десятых становится равной 6,8,
• до сотых – 6,79,
• если округлить до тысячных, то получают 6,786.

Обратите внимание! Незнание этих правил очень удачно используют маркетологи. В магазинах, наблюдая ценник с указанием числа 5,99, большинством покупателей воспринимается цена, равная 5

В действительности же цена товара практически 6.

Математика учимся округлять числа

Правила округления чисел до десятых

Round(Double, MidpointRounding)

Math.Round(d, mode) rounds a double-precision floating-point value to the nearest integer, and uses the specified rounding convention for midpoint values.

Syntax

The syntax of Round(d, mode) method is

Math.Round(Double d, MidpointRounding mode)

where

Parameter	Description
d	The double-precision floating-point number to be rounded.
mode	Specification for how to round the value  if it is midway between two other numbers.

Return Value

The method returns rounded Double value.

Example 8 – Round(Double, MidpointRounding)

In this example, we will take some double-precision floating-point numbers and round them with different modes using Math.Round() method.

C# Program

using System;
 
class Example {
    static void Main(string[] args) {
        Double d, result;

        d = 10.2;
        result = Math.Round(d, MidpointRounding.AwayFromZero);
        Console.WriteLine($"Round({d}, MidpointRounding.AwayFromZero)       = {result}");

        d = 10.8;
        result = Math.Round(d, MidpointRounding.ToEven);
        Console.WriteLine($"Round({d}, MidpointRounding.ToEven)             = {result}");

        d = 10.8;
        result = Math.Round(d, MidpointRounding.ToNegativeInfinity);
        Console.WriteLine($"Round({d}, MidpointRounding.ToNegativeInfinity) = {result}");

        d = 10.2;
        result = Math.Round(d, MidpointRounding.ToPositiveInfinity);
        Console.WriteLine($"Round({d}, MidpointRounding.ToPositiveInfinity) = {result}");

        d = 10.8;
        result = Math.Round(d, MidpointRounding.ToZero);
        Console.WriteLine($"Round({d}, MidpointRounding.ToZero)             = {result}");
    }
}

Output

Round(10.2, MidpointRounding.AwayFromZero)       = 10
Round(10.8, MidpointRounding.ToEven)             = 11
Round(10.8, MidpointRounding.ToNegativeInfinity) = 10
Round(10.2, MidpointRounding.ToPositiveInfinity) = 11
Round(10.8, MidpointRounding.ToZero)             = 10

Conclusion

In this C# Tutorial, we have learnt the syntax of C# Math.Round() method, and also learnt how to use this method with the help of examples.

Округление чисел формулой

Второй способ предполагает реальное округление числа. Для этого используется формулы, с помощью которых задается исходное число, которое нужно округлить и количество знаков после запятой (разрядов), которые нужно сохранить.

Для округления чисел существуют следующие формулы:

=ОКРУГЛ(ячейка; количество разрядов)	Округляет до указанного количества дробных разрядов.
=ОКРУГЛВВЕРХ(ячейка; количество разрядов)	Округляет до ближайшего большего по модулю.
=ОКРУГЛВНИЗ(ячейка; количество разрядов)	Округляет до ближайшего меньшего по модулю значения.

Данные формулы принимают по два аргумента. «Ячейка» — это любое действительное число или адрес ячейки. А «количество разрядом» — это количество знаков после запятой, которые нужно сохранить.

До сотых

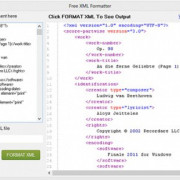
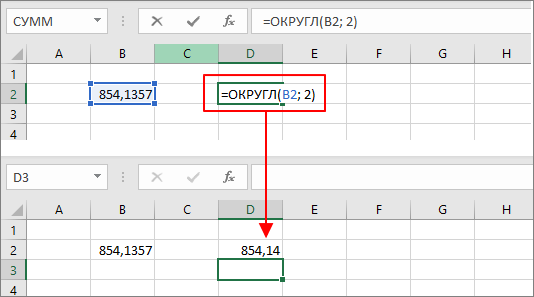
Например, для того чтобы округлить число в ячейке B2 до сотых (до двух разрядов) нужно использовать формулу «=ОКРУГЛ(B2; 2)», где B2 – это адрес ячейки, а второе число «2» — это количество цифр после запятой.

До десятых

Для округления до десятых формула такая же «=ОКРУГЛ(B2; 1)», но во втором аргументе, который указывает на количество цифр после запятой, указываем «1».

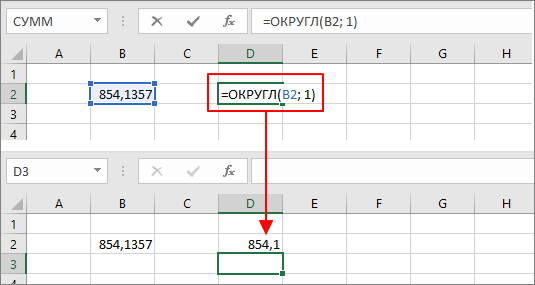
До целого числа

Тоже самое и при округлении до целого числа. Используем ту же формулу «=ОКРУГЛ(B2; 0)», но во втором аргументе указываем «».

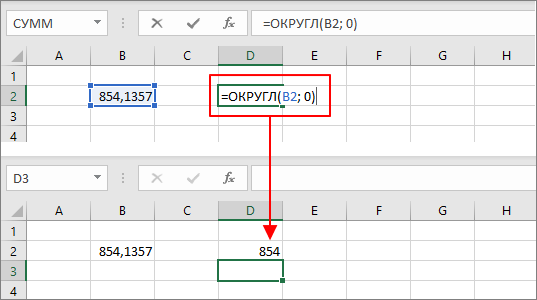
До десятков или сотни

При необходимости данную формулу можно использовать для округления целой части числа до десятков или до сотни. Для этого во втором аргументе нужно указать отрицательное значение. Например, значение «-1» приведет к округлению до десятков, «-2» до сотни и т. д.

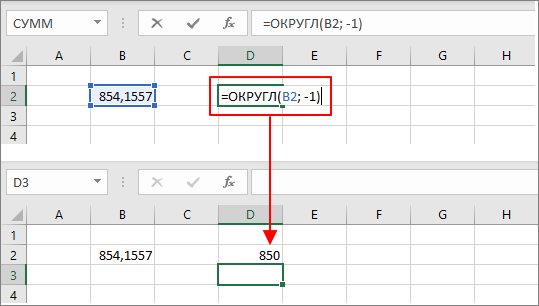
Округление вверх или вниз

Формула «ОКРУГЛ» использует стандартные правила округления, когда в зависимости от значения число может округляться к большему или меньшему значению. Если вам нужно округлить число строго вверх, вне зависимости от самого числа, то следует использовать формулу «=ОКРУГЛВВЕРХ(ячейка; количество разрядов)», а для округления строго вниз нужно использовать формулу «=ОКРУГЛВНИЗ(ячейка; количество разрядов)».

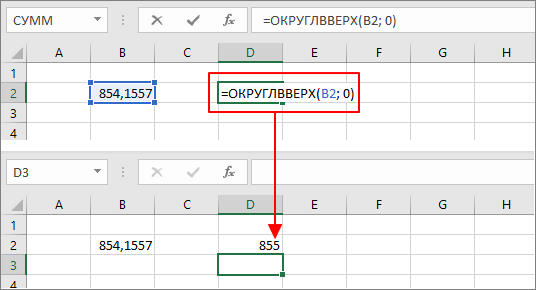
Формулы «ОКРУГЛВВЕРХ» и «ОКРУГЛВНИЗ» работают точно также, как и «ОКРУГЛ». Первый аргумент формулы принимает число или адрес ячейки, а второй – количество цифр после запятой. Для округления до десятков или сотен нужно использовать отрицательные значения.

Округлить до

MulTEx » 13 Январь 2020 Дмитрий 2507 просмотров

Данная функция является частью надстройки MulTEx

Описание, установка, удаление и обновление Полный список команд и функций MulTEx Часто задаваемые вопросы по MulTEx

Вызов команды: MulTEx -группа Ячейки/Диапазоны —Ячейки —Округлить до

Команда округляет все числа в выделенных ячейках до указанного количества десятичных разрядов:

Округлить значения выделенных ячеек до — указывается количество десятичных разрядов, до которого надо округлить число. Например, если в ячейке записано число 45 127,1384. и указано 2, то число будет округлено до двух знаков после запятой, при этом произойдет округление ровно так же, как это делает Excel: 45 127,14. Но есть и другие ситуации — когда округлить надо не просто знаки — а целые числа. К примеру, число 45 127,13 необходимо округлить до тысяч, чтобы получить 45 000. Тогда надо будет указать количество знаков после запятой с минусом: -3. Если число надо просто округлить до целого, то необходимо указать количество знаков после запятой — 0. Диапазон знаков работает от -15 до 15.

Не изменять ячейки с формулами — если установлен, то округление будет производится исключительно для ячеек, не содержащих формулы. Может пригодиться, если на листе перемешаны ячейки с данными, вводимыми вручную и формулами, которые производят вычисления на основании введенных вручную. Тогда можно выделить все ячейки, не задумываясь в каких формулы, а в каких нет, установить флажок Не изменять ячейки с формулами и выполнить команду.

Преобразовывать числа, записанные как текст, в числа — по умолчанию команда игнорирует ячейки, в которых записан текст. При этом если в ячейке записано число, но записано как текст, то команда воспримет его как текст и проигнорирует. Заметка: Что такое число, записанное как текст? Это когда в ячейке отображается число, но по типу данных является текстом. Как правило такие числа помечаются зеленым треугольником в левом верхнем углу ячейки. Формат отображения для таких чисел невозможно изменить напрямую через Формат ячеек, многие функции не учитывают(например СУММ(SUM)).

Если установить флажок Преобразовывать числа, записанные как текст, в числа, то команда Округлить до сама определит такие числа, преобразует их в реальные числа и округлит. Иначе команда будет игнорировать такие числа, считая их текстом.

Так же надо быть осторожным с датами и временем. Т.к. эти данные являются для Excel числовыми, то они так же будут округлены, что может быть нежелательным. Читать подробнее про то, как Excel воспринимает данные >>

Для чего это вообще может быть нужно? Часто при выгрузке документов из других систем и файлов(вроде 1С, файлов CSV, текстовых файлов и т.п.) в Excel числа выгружаются с «хвостами» — 5 и более знаков после запятой: 546 932,78923. Но в ячейке они могут отображаться с округлением — 546 932,79. Как правило это происходит из-за назначенного формата ячеек через Формат ячеек —Число —Числовой —Число десятичных знаков=2:

Это часто приводит к расхождениям расчетов формулами с расчетами на калькуляторе, т.к. на калькуляторе мы суммируем числа с двумя знаками после запятой, а Excel при суммировании формулами учитывает все 5 знаков, т.е. реальное значение числа. Часто в таких ситуациях применяют функции вроде ОКРУГЛ(ROUND), но далеко не всегда это удобно и практично, т.к. формула должна быть записана в другие ячейки. А это приводит к дополнительным неудобствам(создание доп.столбцов, дублирование листов, таблиц и т.п.). С помощью команды Округлить до это можно сделать прямо в этих же ячейках, при этом допускается выделить несколько несмежных ячеек или всю нужную область на листе, вызвать команду и указать нужное количество десятичных разрядов. Так же можно указать, чтобы преобразовывались исключительно ячейки с числами, а ячейки с формулами пропускались. Для этого надо установить флажок Не изменять ячейки с формулами.

Что такое округление?

Округление – это математическая операция, которая позволяет уменьшить количество знаков после запятой в числе, заменив это число его приближенным значением с определенной точностью.

Существуют различные способы округления, такие как округление к большему, округление к меньшему, округление к большему по модулю, округление к меньшему по модулю, случайное округление, чередующееся округление, ненулевое округление, банковское округление.

Наиболее распространенный способ – математическое округление, когда число округляется в меньшую сторону, если в числе «отбрасываемая» цифра меньше пяти и округляется в большую сторону, если в числе «отбрасываемая» цифра больше либо равна пяти.

Остановимся на способах округления и отображения числовых значений, используемых в Excel.

Trivia[]

• C. Round is presumably short for «Checker Round», while K. Round is presumably short for «King Round». Both can also be read as «Crowned.»
• C. Round is the only enemy in Chapter 1 who can be defeated violently without affecting the Chapter 1 ending.
• During battle, C. Round appears to be dancing to music.
• C. Round becoming K. Round is a reference to American Checkers

  However, it does so by moving forward orthogonally, which is an illegal move in checkers.

  , in which pieces can be «kinged» by reaching the far end of the board. Kinged pieces gain both a «crown,» usually another checker placed atop the first one to visibly differentiate it from uncrowned pieces, and increased mobility, a powerful advantage.

• While only a red C. Round is seen in the Dark World, both red and black checkers are strewn on the board in the Empty Classroom.
• If Susie’s attack stat is edited in the save data, C. Round can survive one hit, but this causes it to become tired the next turn. Attempting to «Pacify» it causes the game to crash due to the game attempting to display the spared sprite for C. Round, which doesn’t exist. C. Round never attacks, even if it survives multiple turns.
• If the damage of the party is modified by external means, it is possible to «kill» K. Round, knocking it back much like C. Round, by outdamaging its heal. However, this does not generate any additional dialogue or alter the story, as it is not supposed to happen.
• K. Round is the only boss without any dialogue.
• It is possible to interact with the control crown as it slides away after the second K. Round battle by using the Wrist Protector to skip the post-battle text. The first interaction brings up «(Thar she blows…)» and further interactions bring up «(It’s going off to live a better life now…)«
• The growing and shrinking sound effects of K. Round are a reference to the Super Mushroom sound effects from the Mario series.
• There was merchandise planned for K. Round, but it was scrapped after people pointed out that K. Round bore a striking resemblance to the Japanese mascot, Nishiko-kun (にしこくん).

Модули для вычислений с плавающей запятой

Есть четыре популярных модуля, которые помогут вам правильно работать с числами с плавающей запятой. Сюда входят модули math, Numpy, decimal и fraction.

Математический модуль (math) сосредоточен на математических константах, операциях с плавающей запятой и тригонометрических методах. Модуль Numpy описывает себя как «фундаментальный пакет для научных вычислений» и известен своим разнообразием методов работы с массивами. Модуль decimal охватывает десятичную арифметику с фиксированной и плавающей запятой, а модуль fraction имеет дело, в частности, с рациональными числами.

Во-первых, мы должны попытаться улучшить вычисления из примера 1. Как показано в примере 7, после импорта математического модуля мы можем получить доступ к методу fsum(), который принимает список чисел с плавающей запятой. Для первого вычисления нет разницы между встроенным методом sum() и методом fsum() из математического модуля, но для второго – он возвращает правильный результат, которого мы ожидали. Точность зависит от базового алгоритма IEEE 754.

Пример 7: вычисления с плавающей запятой с помощью модуля math

>>> import math
>>> sum()
0.30000000000000004
>>> math.fsum()
0.30000000000000004
>>> sum()
0.9999999999999999
>>> math.fsum()
1.0

Во-вторых, давайте посмотрим на модуль Numpy. Он поставляется с методом around(), который округляет значения, предоставленные в виде массива. Он обрабатывает отдельные значения так же, как метод round() по умолчанию.

Для сравнения значений Numpy предлагает метод equal(). Как и around(), он принимает отдельные значения, а также списки значений (так называемые векторы) для обработки. В примере 8 показано сравнение отдельных значений, а также округленных. Наблюдаемое поведение очень похоже на ранее показанные методы.

Пример 8: сравнение значений с использованием метода equal из модуля Numpy

>>> import numpy
>>> print (numpy.equal(0.3, 0.3))
True
>>> print (numpy.equal(0.3 + 0.3 + 0.3 , 0.9))
False
>>> print (numpy.equal(round(0.3 + 0.3 + 0.3) , round(0.9)))
True

Вариант третий – десятичный модуль (decimal). Он предлагает точное десятичное представление и сохраняет значащие цифры. По умолчанию точность составляет 28 цифр, и вы можете изменить это значение на число, которое будет настолько большим, насколько это необходимо для вашей проблемы. В примере 9 показано, как использовать точность до 8 цифр.

Пример 9: создание десятичных чисел с помощью модуля decimal

>>> import decimal
>>> decimal.getcontext().prec = 8
>>> a = decimal.Decimal(1)
>>> b = decimal.Decimal(7)
>>> a / b
Decimal('0.14285714')

Теперь сравнение значений с плавающей запятой стало намного проще и привело к желаемому результату.

Пример 10: сравнение с использованием модуля Decimal

>>> import decimal
>>> decimal.getcontext().prec = 1
>>> a = decimal.Decimal(0.3)
>>> b = decimal.Decimal(0.3)
>>> c = decimal.Decimal(0.3)
>>> a + b + c
Decimal('0.9')
>>> a + b + c == decimal.Decimal('0.9')
True

Модуль decimal также имеет метод округления значений – quantize(). Стратегия округления по умолчанию – округление от половины до четного, и при необходимости ее также можно изменить на другой метод. В примере 11 показано использование метода quantize()

Обратите внимание, что количество цифр указывается с использованием десятичного значения в качестве параметра.

Пример 11: округление значения с помощью quantize()

>>> d = decimal.Decimal(4.6187)
>>> d.quantize(decimal.Decimal("1.00"))
Decimal('4.62')

И последнее, но не менее важное: мы рассмотрим модуль fractions. Этот модуль позволяет обрабатывать значения с плавающей запятой как дроби, например 0,3 как 3/10

Это упрощает сравнение значений с плавающей запятой и полностью исключает округление значений. В примере 12 показано, как использовать модуль fractions.

Пример 12: хранение и сравнение значений с плавающей запятой

>>> import fractions
>>> fractions.Fraction(4, 10)
Fraction(2, 5)
>>> fractions.Fraction(6, 18)
Fraction(1, 3)
>>> fractions.Fraction(125)
Fraction(125, 1)
>>> a = fractions.Fraction(6, 18)
>>> b = fractions.Fraction(1, 3)
>>> a == b
True

Кроме того, два модуля десятичной дроби и дроби можно комбинировать, как показано в следующем примере.

Пример 13: работа с десятичными знаками и дробями

>>> import fractions
>>> import decimal
>>> a = fractions.Fraction(1,10)
>>> b = fractions.Fraction(decimal.Decimal(0.1))
>>> a,b
(Fraction(1, 10), Fraction(3602879701896397, 36028797018963968))
>>> a == b
False

Поля

AwayFromZero	1	Стратегия округления до ближайшего числа, а если число находится на расстоянии от двух других, оно округляется в сторону ближайшего числа, которое находится вне нуля.
ToEven	Стратегия округления до ближайшего числа, а если число находится на расстоянии от двух других, оно округляется в сторону ближайшего четного числа.
ToNegativeInfinity	3	Стратегия нисходящей, направленная вниз, с результатом, наиболее близким к и не превышающим бесконечно точный результат.
ToPositiveInfinity	4	Стратегия сквозного округления с результатами, ближайшей к и не меньше бесконечно точных результатов.
ToZero	2	Стратегия направленного округления в сторону нуля с результатом, наиболее близким к и не превышающим точность, чем бесконечное значение.

Оператор Round

А вы знаете, что при использовании для округления чисел в VBA Excel оператора Round, вы можете получить совершенно не тот результат, который ожидали? И ведь это действительно так!

Скопируйте в модуль VBA следующую процедуру и запустите ее выполнение:

1 2 3 4 5 6 7 8 9 10 11

SubTest_1() Dima1 AsSingle,a2 AsSingle,a3 AsSingle,a4 AsSingle a1=Round(1.5,) a2=Round(2.5,) a3=Round(3.5,) a4=Round(4.5,) MsgBox»Round(1.5, 0)=»&a1&vbNewLine&_ «Round(2.5, 0)=»&a2&vbNewLine&_ «Round(3.5, 0)=»&a3&vbNewLine&_ «Round(4.5, 0)=»&a4 EndSub

В результате вы получите это:

Удивительно, не правда ли? Как же так получилось?
Дело в том, что оператор Round осуществляет «бухгалтерское» (или «банковское») округление, которое призвано при большом количестве таких операций свести погрешность к минимуму. Это достигается за счет того, что оператор Round использует при округлении правило, отличное от того, которое мы знаем еще со школы, когда округляемое число увеличивается на единицу, если отбрасываемое число равно пяти. Суть округления с помощью оператора Round состоит в том, что если перед отбрасываемой пятеркой стоит нечетная цифра, то она увеличивается на единицу (округление вверх), а если перед ней стоит четная цифра, то она не увеличивается (округление вниз).

Еще можно сформулировать «бухгалтерское» округление так: при отбрасывании пятерки число округляется к ближайшему четному

Обратите внимание, что в результатах нашего примера все полученные числа — четные.
Проверим погрешность:

1. Сумма исходных чисел: 1.5 + 2.5 + 3.5 +4.5 = 12
2. Сумма округленных чисел: 2 + 2 + 4 + 4 = 12

Результат получился просто идеальный для приведенного примера, так как суммы исходных и округленных чисел равны.