Три способа умножения матриц в excel — fastai part-2, lesson-8

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

 

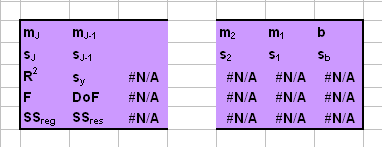
Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

Способ 1: использование 3-х циклов FOR

Вот еще один отказ от ответственности, при реализации умножения матриц в Excel, мы не только поняли это, но и повторили первый метод Джереми, который использовал 3 цикла FOR. Вот как это выглядит в коде:

def matmul1(a,b):    ar,ac = a.shape    br,bc = b.shape    assert ac==br    c = torch.zeros(ar, bc)    for i in range(ar):        for j in range(bc):            for k in range(ac): #or br                c += a*b    return c

Надеюсь, теперь вы сможете лучше понять это. Если нет, то сейчас самое время сделать паузу, поэкспериментировать с кодом и посмотреть, что на самом деле происходит. Я обещаю вам, это так же, как наша версия Excel!

Хорошо, я предполагаю, что вы потратили некоторое время на размышления о коде, поэтому давайте обсудим это!

• Почему первые две петли ва также? Ну, как вы помните изПравило-2наша результирующая матрица будет иметь размеры, И из Excel мы увидели, что мы пересекаем каждый элементСследовательно, один за другим, чтобы пройтистроки истолбцы нам нужно 2 цикла ва также,
• Итак, почему третий цикл FOR в? Ну изПравило-1, мы знаем этотак что на самом деле не имеет значения, ставим ли мыилив третьем цикле. По сути, именно здесь отдельные элементы умножаются вместе и добавляются. Из нашего предыдущего примера Excel, дляэто где шагпроизойдет, и, наконец, мы перейдем к следующей коробке. Количество предметов, которые умножаются и складываются вместе, равно,

Это действительно так! Это метод-1 для вас! Вот песня, чтобы помнить Матричное Умножение. (Я узнал об этом первым из fast.ai, оригинальный автор неизвестен)

Надеюсь, теперь вы понимаете, как две матрицы умножаются друг на друга. Если не,Вотэто еще один учебник Хан Академии

Операции с массивами

Массив – это группа данных, которая расположена на листе в смежных ячейках. По большому счету, любую таблицу можно считать массивом, но не каждый из них является таблицей, так как он может являться просто диапазоном. По своей сущности такие области могут быть одномерными или двумерными (матрицы). В первом случае все данные располагаются только в одном столбце или строке.

Во втором — в нескольких одновременно.

Кроме того, среди одномерных массивов выделяют горизонтальный и вертикальный тип, в зависимости от того, что они собой представляют – строку или столбец.

Нужно отметить, что алгоритм работы с подобными диапазонами несколько отличается от более привычных операций с одиночными ячейками, хотя и общего между ними тоже много. Давайте рассмотрим нюансы подобных операций.

Создание формулы

Формула массива – это выражение, с помощью которого производится обработка диапазона с целью получения итогового результата, отображаемого цельным массивом или в одной ячейке. Например, для того, чтобы умножить один диапазон на второй применяют формулу по следующему шаблону:

Над диапазонами данных можно также выполнять операции сложения, вычитания, деления и другие арифметические действия.

Координаты массива имеют вид адресов первой её ячейки и последней, разделенные двоеточием. Если диапазон двумерный, то первая и последняя ячейки расположены по диагонали друг от друга. Например, адрес одномерного массива может быть таким: A2:A7.

А пример адреса двумерного диапазона выглядит следующим образом: A2:D7.

1. Чтобы рассчитать подобную формулу, нужно выделить на листе область, в которую будет выводиться результат, и ввести в строку формул выражение для вычисления.

После ввода следует нажать не на кнопку Enter, как обычно, а набрать комбинацию клавиш Ctrl+Shift+Enter. После этого выражение в строке формул будет автоматически взято в фигурные скобки, а ячейки на листе будут заполнены данными, полученными в результате вычисления, в пределах всего выделенного диапазона.

Изменение содержимого массива

Если вы в дальнейшем попытаетесь удалить содержимое или изменить любую из ячеек, которая расположена в диапазоне, куда выводится результат, то ваше действие окончится неудачей. Также ничего не выйдет, если вы сделаете попытку отредактировать данные в строке функций. При этом появится информационное сообщение, в котором будет говориться, что нельзя изменять часть массива. Данное сообщение появится даже в том случае, если у вас не было цели производить какие-либо изменения, а вы просто случайно дважды щелкнули мышью по ячейке диапазона.

Если вы закроете, это сообщение, нажав на кнопку «OK», а потом попытаетесь переместить курсор с помощью мышки, или просто нажмете кнопку «Enter», то информационное сообщение появится опять. Не получится также закрыть окно программы или сохранить документ. Все время будет появляться это назойливое сообщение, которое блокирует любые действия. А выход из ситуации есть и он довольно прост

1. Закройте информационное окно, нажав на кнопку «OK».

Затем нажмете на кнопку «Отмена», которая расположена в группе значков слева от строки формул, и представляет собой пиктограмму в виде крестика. Также можно нажать на кнопку Esc на клавиатуре. После любой из этих операций произойдет отмена действия, и вы сможете работать с листом так, как и прежде.

Но что делать, если действительно нужно удалить или изменить формулу массива? В этом случае следует выполнить нижеуказанные действия.

Для изменения формулы выделите курсором, зажав левую кнопку мыши, весь диапазон на листе, куда выводится результат

Это очень важно, так как если вы выделите только одну ячейку массива, то ничего не получится. Затем в строке формул проведите необходимую корректировку. После того, как изменения внесены, набираем комбинацию Ctrl+Shift+Esc

Формула будет изменена.

После того, как изменения внесены, набираем комбинацию Ctrl+Shift+Esc. Формула будет изменена.

1. Для удаления формулы массива нужно точно так же, как и в предыдущем случае, выделить курсором весь диапазон ячеек, в котором она находится. Затем нажать на кнопку Delete на клавиатуре.

После этого формула будет удалена со всей области. Теперь в неё можно будет вводить любые данные.

Определение умножения

Рассмотрим две согласованные матрицы: $A=\left$ и $B=\left$. И определим для них операцию умножения.

По-моему, тут всё очевидно. Дальше можно не читать.

У тех, кто впервые видит это определение, сразу возникает два вопроса:

1. Что это за лютая дичь?
2. А почему так сложно?

Что ж, обо всём по порядку. Начнём с первого вопроса. Что означают все эти индексы? И как не ошибиться при работе с реальными матрицами?

Прежде всего заметим, что длинная строчка для расчёта ${{c}_{i;j}}$ (специально поставил точку с запятой между индексами, чтобы не запутаться, но вообще их ставить не надо — я сам задолбался набирать формулу в определении) на самом деле сводится к простому правилу:

1. Берём $i$-ю строку в первой матрице;
2. Берём $j$-й столбец во второй матрице;
3. Получаем две последовательности чисел. Перемножаем элементы этих последовательностей с одинаковыми номерами, а затем складываем полученные произведения.

Данный процесс легко понять по картинке:

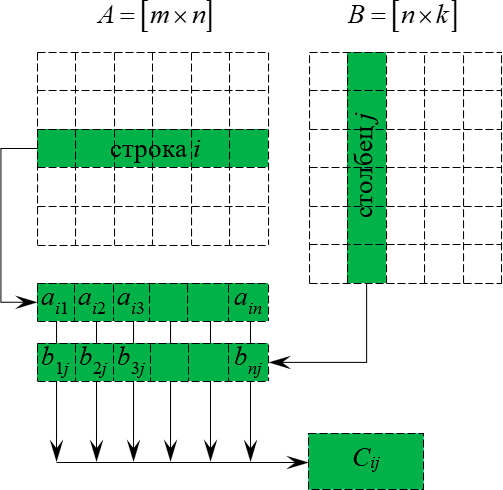Схема перемножения двух матриц

Ещё раз: фиксируем строку $i$ в первой матрице, столбец $j$ во второй матрице, перемножаем элементы с одинаковыми номерами, а затем полученные произведения складываем — получаем ${{c}_{ij}}$. И так для всех $1\le i\le m$ и $1\le j\le k$. Т.е. всего будет $m\times k$ таких «извращений».

Но хватит теории! Давайте посмотрим на реальные примеры. И начнём с самого простого случая — квадратных матриц.

Метод 3: вещание

Заметили общую тему здесь? Каждый раз мы должны умножить каждый рядс каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и тот же вектор строки враз! И мы повторяем этот процессраз!

Есть ли способ умножить вектор строкисо всеми столбцамиВполучить соответствующий ряд вC?Да, есть! Войдите в трансляцию …Примечание: я не буду объяснять вещание, Джереми делает это очень хорошоВот,

Вместо этого давайте посмотрим, что это за волшебный кусок кода

for i in range(ar):        c = (a.unsqueeze(-1).expand_as(b)*b).sum(dim=0)

Как обычно, давайте повторим в Excel! Это сделает вещи действительно легкими. Давайте сделаем это поэтапно.

Шаг 1)Выберите i-й ряд, Мы выбираем строку 0 в качестве примера.

Выберите строку 0 из

Шаг 2)Возьмите егоТранспонирование

Возьмите транспонирование строки 0 из A

Шаг 3)Развернуть матрицу столбца какВ

Развернуть матрицу столбца как B

Шаг-4)Элемент мудрый умножить наВ

Умножить элемент на B

Шаг-5)Суммируйте по строкам, чтобы получить строку 0 C

Суммируйте по измерению боковой строки, чтобы получить строку 0 C

Полный процесс вещания для каждого рядавыглядит примерно так:

Вещание в целом

Я надеюсь, что теперь вы получитевещания!Итак, давайте посмотрим, как это выглядит в коде ..

def matmul3(a,b):    ar,ac = a.shape    br,bc = b.shape    assert ac==br    c = torch.zeros(ar,bc)    for i in range(ar):        c = (a.unsqueeze(-1).expand_as(b)*b).sum(dim=0)        print(f"i:{i}")        print(c)    return c

Вывод выглядит так:

i:0tensor(,        ,        ,        ])i:1tensor(,        ,        ,        ])i:2tensor(,        ,        ,        ])i:3tensor(,        ,        ,        ])

Это именно то, как мы ожидаем, что это будет так же, как нашиВерсия Excel!

Вот и все! Мы успешно рассмотрели три метода умножения матриц, включая вещание.

Google лист для вышеупомянутой иллюстрации можно найтиВот, Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресуhttps://linkedin.com/in/aroraaman/,

3.2. Пример

Рассмотрим вопрос о применении средств VBA на примере.

При моделировании неизотермической кинетики (ДСК, ТГА, и
т.п.) необходима
интегральная показательная функция (integral
exponential) E₁(x). По определению,

Для вычисления E₁(x) можно
использовать бесконечный ряд  

На листе рабочей книги Excel каждый член этого ряда
можно поместить в отдельную ячейку и затем просуммировать их. Этот
способ показан на Рис. 41.  

Рис.41 Вычисление функции E₁(x)
на листе

Нельзя признать такой способ вычисления удачным.
Во-первых, вычисления занимают на листе много места. Но главное, не
понятно, сколько членов в ряду нужно суммировать – иногда хватит и 10, а
иногда и 50 будет мало.

1.7. Некоторые важные функции

Excel предоставляет широкий выбор стандартных
(встроенных) функций. Мы не можем рассмотреть их все, поэтому
остановимся только на тех, которые представляются нам самыми важными.

SUM/ СУММ

Суммирует все числа в
списке аргументов или в области.

Синтаксис:

SUM(number1
) 

Пример

Рис.12
Функция SUM

SUMSQ / СУММКВ

Возвращает сумму квадратов аргументов.

Синтаксис:

SUMSQ(number1
) 

Пример

Рис.13 Функция SUMSQ

SUMPRODUCT / СУММПРОИЗВ

Перемножает соответствующие элементы заданных массивов и
возвращает сумму произведений

Синтаксис:

SUMPRODUCT (array1,
array2, …)  

Пример

Рис.14 Функция SUMPRODUCT

AVERAGE / СРЗНАЧ

Возвращает
своих аргументов

Синтаксис:

AVERAGE(number1
) 

Пример

Рис.15 Функция AVERAGE

VAR / ДИСП 

Оценивает по выборке .

Синтаксис:

VAR(number1
,number2,

…) 

Пример
 

Рис.16 Функция VAR

STDEV / СТАНДОТКЛОН

Оценивает по выборке
.

Синтаксис:

STDEV(number1
,number2,

…) 

Пример

Рис.17 Функция
STDEV

CORREL / КОРРЕЛ

Возвращает
между интервалами
ячеек array1 и array2

Синтаксис:

CORREL(array1,
array2)

Пример

Рис.17 Функция
CORREL

Функции можно объединять в
составные формулы, пример которой показан на Рис. 19.

Рис.19 Пример составной формулы

Простые операции в Excel: сложение, вычитание

≡  14 Апрель 2016   ·  Рубрика: Могучий MS Excel   

Excel – универсальный инструмент, сложный программный продукт, используемый в различных отраслях.

Но какие-бы сложные инструменты вы не использовали, без простых формул, содержащих элементарные математические операции, вам не обойтись.

Далее я расскажу о том, как делать формулы, содержащие операции сложения и вычитания.

Сложение в Excel – одна из наиболее частых операций, применяемых для создания формул. Рядом со сложением смело можно поставить операцию вычитания. По своему алгебраическому смыслу операции идентичны, но имеют «разный знак». Простейшие алгебраические формулы, которые мы часто видели на школьной доске, выглядят следующим образом.

Простые операции в алгебре

Возможно вы не поверите, но то что вы видели в школе на доске, немногим будет сложнее сделать в Excel. Прежде всего, нужно уяснить, что любая формула в Excel делается по следующим правилам и понятиям:

1. Весь лист разбит на ячейки, и к каждой ячейке можно обратится по адресу. Обычно адрес ячейки выглядит так «А1», «В7». Эти адреса означают, что ячейка находится в столбце А и строке 1 или столбце В и строке 7.
2. Если нужно записать любую формулу, то она записывается в ячейку.
3. В том случае если используются простые операции, тогда, для того, чтобы перейти в режим ввода формулы, нужно поставить знак «=».
4. По завершению ввода формулы нужно нажать «Ввод»
5. В ячейке будет виден результат выполнения формулы, а не сама формула.

Простая операция: сложение, вычитание

Теперь построим формулы сложения и вычитания в Excel.

Допустим: значение А хранится в ячейке «А1», значение В в ячейке В1. В ячейку С1 нужно записать результат суммы А1 и В1, а в ячейке С2 произвести вычитание В1 из А1.

• Формулы сложения и вычитания будут выглядеть так.
• =А1+В1
• =А1-В1

Вид формулы сложения

Вид формулы вычитания

Все четко видно на картинках, хочется только добавить  — не забывайте нажимать Ввод после окончания ввода любой формулы, не обязательно сложения или вычитания. И понятно, что для сложения используется символ «+», для вычитания символ «-».

Сложные варианты сложения: Функция СУММ()

Одним из сложных вариантов является прибавление процентов. Из-за сложности вопроса я написал отдельную статью.

КАК ПРИБАВИТЬ ПРОЦЕНТЫ В EXCEL С ПОМОЩЬЮ ФОРМУЛЫ

Прежде всего, нужно рассмотреть сложение ячеек по столбцу. Наилучший способ использование в формуле функции «СУММ». Этой функции передается диапазон ячеек и/или указываются, через точку с запятой, ячейки, по которым нужно провести суммирование.

Вид задания

Посмотрите на рисунок, условия задачи таковы: в ячейку F6 нужно записать сумму чисел записанных в диапазоне С1:С5, прибавить D1 и прибавить диапазон чисел записанный в D3:D5.

1. Становимся курсором в позицию F6 и нажимаем на кнопку «Вставить функцию».
2. В открывшемся окне «Мастер функций», есть поле поиск функции , в него мы записываем «Сумм»(без кавычек) и нажимаем кнопку «Ок»(в диалоговом окне)!

Мастер функций

После проделанных действий откроется другое диалоговое окно «Аргументы функции».

Теперь для функции сумм нужно установить параметры – диапазоны и ячейки для суммирования

Обращаю внимание, что таких параметров может быть 255 и при ручном вводе разделять их нужно символом «;»

Аргументы функций

После нажатия на кнопке , в ячейке F6 будет записана формула содержащая функцию суммирования, но пользователь увидит результат суммирования.

Думаю, прочитав эту статью, вы убедились, что операции сложения и вычитания это очень просто. Могу лишь посоветовать экспериментировать, экспериментировать и еще …

Транспонирование

Транспонировать матрицу – поменять строки и столбцы местами.

Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области.

1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК.

2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей.

Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter.

Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица.

Сложение

Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона.

В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+H2). Нажать Enter и растянуть формулу на весь диапазон.

Умножение матриц в Excel

Условие задачи:

Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной).

Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй.

В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй.

Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Обратная матрица в Excel

Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое).

Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР.

Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД.

Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.

Метод 2: Использование поэлементного умножения

Так что до сих пор мы разбираем каждую позицию в результирующей матрицеC,найти отдельные элементы, а затем суммировать их вместе. Если вы помните, что-то вроде, Конечно, должен быть другой путь? Что если вместо того, чтобы делать отдельные продукты, а затем суммировать их, мы умножаем векторы за один раз, чтобы получить результирующий вектор, и суммируем полученный вектор, чтобы получить конечный элемент?

m = tensor()n = tensor()m*n>>tensor()

До сих пор мы находили отдельные продуктыи сложить их вместе, Но, действительно, все это можно заменить на:

m = tensor()n = tensor()(m*n).sum()>>tensor(60)

Если вы помните, самый внутренний цикл внаходил отдельные продукты и добавлял их. Ну, мы можем заменить этот цикл, чтобы выполнить векторное поэлементное произведение и положитьв конце концов, и PyTorch / NumPy имеют возможность выполнять поэлементные операции для нас!

Вот как это выглядит в Excel:

C = сумма (A * B )

Точно так же мы получаемпутем умножения вектора в строке 0с вектором на цв 3Ви суммируя полученный вектор.

C = сумма (A * B )

И, наконец, мы следуем тому же процессу, чтобы пройти каждый пустой ящик вСчтобы получить окончательный результат.

C = сумма (A * B )

Обратите внимание, как это отличается отМетод-1? На этот раз мы просто говорим Excel или PyTorch: умножьте строку 0с col 0 изВи суммируем полученный вектор, чтобы дать нам ответ. Вместо того чтобы делать, Например, дляэтот метод умножает Vector на строку 0с вектором в столбце 0 изВчтобы получить промежуточный продукт Вектори суммирует это, чтобы дать результат в положениикак,. В коде это выглядит так:

В коде это выглядит так:

def matmul2(a,b):    ar,ac = a.shape    br,bc = b.shape    assert ac==br    c = torch.zeros(ar,bc)    for i in range(ar):        for j in range(bc):            c = (a*b).sum()    return c

Таким образом, мы просто анализируем каждую позициюC,используя две петли FOR и введите соответствующий результат в этой позиции. Еслипредставляют строки и столбцы вСэто выглядит примерно так …

i:0,j:0a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:0,j:1a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:0,j:2a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:0,j:3a:tensor(),b:tensor()tensor(,        ,        ,        ])---i:1,j:0a:tensor(),b:tensor()tensor(,        ,        ,        ])

И так далее .. пока мы не получим полную матрицуС,

tensor(,        ,        ,        ])

2.1. Формулы массива

Многие операции с матрицами выполняются с помощью формул
специального вида, называемыми формулами массива. От других формул они
отличаются тем, что их результатом является не одна величина (число), а
набор величин – массив. При вводе таких формул требуется специальное
подтверждение – вместо клавиши ENTER надо
нажимать комбинацию из трех клавиш CTRL+SHIFT+ENTER.

Поясним использование формул массивов на простом
примере. Предположим, что нам нужно выполнить автошкалирование
(стандартизацию) данных, записанных в матрице X. Для
этого сначала нужно вычислить средние значения m_j и
среднеквадратичные отклонения s_j для каждого (j-го)
столбца X, а затем вычесть из каждого столбца величину
m_jи поделить на величину s_j

Такое преобразование можно сделать с помощью обычных формул, как это
показано на Рис. 25.

Рис.25
Обычная формула

Надо только не забыть указать знак $ перед номерами строк
9 (m) и 11
(s) , чтобы зафиксировать положение соответствующих величин в
строках.

Если матрица X велика, то удобнее
воспользоваться формулой массива. (Рис. 26). Назовем соответствующие
области на листе: X,
m и
s. Отметим пустую область
N3:R7, размеры которой совпадают с ожидаемым результатом. После
этого введем в Formula Bar  выражение
=(X-m)/s. Завершает ввод комбинация клавиш
CTRL+SHIFT+ENTER. Если все сделано правильно,
то в Formula Bar появится формула
{ =(X-m)/s}, заключенная в фигурные скобки
{}. Это – признак формулы массива. .

Рис.26
Формула массива

Видеоурок

Учитель физики, информатики и ИКТ, МКОУ «СОШ», с. Саволенка Юхновского района Калужской области. Автор и преподаватель дистанционных курсов по основам компьютерной грамотности, офисным программам. Автор статей, видеоуроков и разработок.

В разделе на вопрос Как создать матрицу в Excel???? заданный автором Masha Kalganova
лучший ответ это Что конкретно нужно сделать?Документ эксель — безразмерная (всеразмерная) матрица, каждый элемент которой может быть числом, текстом или любым другим значением. Да хоть формулой.Если напечатать 3 циферки в ряд, под ними еще 3 в ряд, под ними еще 3 в ряд, получим квадратную матрицу 3х3.Вопрос в чем?Умножение матрицы на число в ExcelФормулы написать?В верхней левой клетке новой матрицы=левая верхняя клетка старой матрицы * клетка с числом (ткнуть мышкой) , нажать F4 дабы стало $x$y, где x,y — координаты клетки. Это зафиксирует клетку при копировании. Далее жмем Enter и копируем содержимое клетки в 2 соседние клетки в ряд. Далее копируем эти 3 клетки в следующие 3 ряда и получаем тот же результат, что у меня на картинке. То есть умножение матрицы на число.Блин, математику не знают, а в интернете лазают!

В программе Excel с матрицей можно работать как с диапазоном. То есть совокупностью смежных ячеек, занимающих прямоугольную область.

Адрес матрицы – левая верхняя и правая нижняя ячейка диапазона, указанные черед двоеточие.

Выполнение расчетов

Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.

Расчет определителя

Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.

1. Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.
2. Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
3. Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».
4. Программа производит расчет определителя. Как видим, для нашего конкретного случая он равен – 59, то есть не тождественен нулю. Это позволяет сказать, что у данной матрицы существует обратная.

Расчет обратной матрицы

Теперь можно преступить к непосредственному расчету обратной матрицы.

1. Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
2. В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».
3. В поле «Массив», открывшегося окна аргументов функции, устанавливаем курсор. Выделяем весь первичный диапазон. После появления его адреса в поле, жмем на кнопку «OK».
4. Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
5. Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.

На этом расчет можно считать завершенным.

Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.

Мы рады, что смогли помочь Вам в решении проблемы.

Помогла ли вам эта статья?

Нахождение обратной матрицы всегда вызывало большие затруднения у учащихся, так как это был очень трудоемкий процесс. И вот такое задание вполне по силам EXCEL.  

Прежде всего, уясним одно правило:  Матрица имеет обратную только тогда, когда ее определитель не равен нулю.  А вот и задание: найдите матрицу, обратную к матрице А, где

Вычислять определитель этой матрицы мы умеем. Я его уже вычислил.

Он оказался равен -4, а  это значит, что у нашей матрицы есть обратная (если бы определитель оказался равен нулю, то мы сказали бы что матрица не имеет обратную и немедленно прекратили все вычисления). Теперь отметим ячейку, с которой начнем записывать ответ. Я отметил ячейку E1.  Нажимаем Формулы, затем Математические и в появившемся окне находим  МОБР

После нажатия появляется вот такое окно, в котором надо вписать адреса ячеек, в которых находятся элементы матрицы  в Массив

У нас элементы записаны в ячейки начиная с А1 и заканчивая в С3 , поэтому так и записываем (смотрите картинку)

Если все сделали правильно, то автоматически заполнится место, обведенное красным и запишется ответ, который обведен черным. В таком виде ответ трудно переваривать и поэтому нажимаем ОК.  В ячейке, которую мы застолбили под ответ, появилось число 3,  Это только первый элемент полученной обратной матрицы.

Чтобы виден был весь ответ, выполняем следующие действия: Начиная с  ячейки Е1 выделяем три строчки и три столбца (именно столько было у исходной матрицы и столько же будет у обратной)

нажимаем клавишу F2,  а затем на одновременно на три клавиши  Ctrl+Shift+Enter.

В выделенном месте появляются, теперь уже все, элементы обратной матрицы. Если Вы сохраните этот документ, то в следующий раз можете воспользоваться плодами своего труда. Так, меняя элементы исходной матрицы, Вы автоматически получаете для нее же обратную матрицу.

На этом все. Крепких вам знаний.

Рубрика: EXCEL в помощь, Статьи. Метки: EXCEL, ИКТ, матрица, обратная матрица

Основные свойства матричного произведения

В двух словах. Умножение матриц:

1. Некоммутативно: $A\cdot B\ne B\cdot A$ в общем случае. Бывают, конечно, особые матрицы, для которых равенство $A\cdot B=B\cdot A$ (например, если $B=E$ — единичной матрице), но в абсолютном большинстве случаев это не работает;
2. Ассоциативно: $\left( A\cdot B \right)\cdot C=A\cdot \left( B\cdot C \right)$. Тут без вариантов: стоящие рядом матрицы можно перемножать, не переживая за то, что стоит левее и правее этих двух матриц.
3. Дистрибутивно: $A\cdot \left( B+C \right)=A\cdot B+A\cdot C$ и $\left( A+B \right)\cdot C=A\cdot C+B\cdot C$ (в силу некоммутативности произведения приходится отдельно прописывать дистрибутивность справа и слева.

А теперь — всё то же самое, но более подробно.

Умножение матриц во многом напоминает классическое умножение чисел. Но есть отличия, важнейшее из которых состоит в том, что умножение матриц, вообще говоря, некоммутативно.

Рассмотрим ещё раз матрицы из задачи 1. Прямое их произведение мы уже знаем:

\\cdot \left=\left\]

Но если поменять матрицы местами, то получим совсем другой результат:

\\cdot \left=\left\]

Получается, что $A\cdot B\ne B\cdot A$. Кроме того, операция умножения определена только для согласованных матриц $A=\left$ и $B=\left$, но никто не гарантировал, что они останутся согласованными, если их поменять местами. Например, матрицы $\left$ и $\left$ вполне себе согласованы в указанном порядке, но те же матрицы $\left$ и $\left$, записанные в обратном порядке, уже не согласованы. Печаль.:(

Тем не менее, умножение матриц ассоциативно:

\

Следовательно, когда вам надо перемножить сразу несколько матриц подряд, совсем необязательно делать это напролом: вполне возможно, что некоторые рядом стоящие матрицы при перемножении дают интересный результат. Например, нулевую матрицу, как в Задаче 2, рассмотренной выше.

В реальных задачах чаще всего приходится перемножать квадратные матрицы размера $\left$. Множество всех таких матриц обозначается ${{M}^{n}}$ (т.е. записи $A=\left$ и \ означают одно и то же), и в нём обязательно найдётся матрица $E$, которую называют единичной.

Идём далее. Помимо ассоциативности умножение матриц ещё и дистрибутивно:

\

Другими словами, если нужно умножить одну матрицу на сумму двух других, то можно умножить её на каждую из этих «двух других», а затем результаты сложить. На практике обычно приходится выполнять обратную операцию: замечаем одинаковую матрицу, выносим её за скобку, выполняем сложение и тем самым упрощаем себе жизнь.:)

Заметьте: для описания дистрибутивности нам пришлось прописать две формулы: где сумма стоит во втором множителе и где сумма стоит в первом. Это происходит как раз из-за того, что умножение матриц некоммутативно (и вообще, в некоммутативной алгебре куча всяких приколов, которые при работе с обычными числами даже не приходят в голову). И если, допустим, вам на экзамене нужно будет расписать это свойство, то обязательно пишите обе формулы, иначе препод может немного разозлиться.

Ладно, всё это были сказки о квадратных матрицах. А что насчёт прямоугольных?

1.10. Построение графиков

В Excel можно строить диаграммы разных типов. Но для нас
интересны только два вида: диаграмма рассеяния (scatter) и  график (line).
Пример диаграммы рассеяния приведен на Рис. 24 .

Рис.24
Диаграмма рассеяния

Диаграммы такого типа используются для построения графиков
счетов, зависимостей «измерено-предсказано», и т.п. От линейных графиков
они отличаются равноправием обеих осей. В линейных графиках ось абсцисс
предназначена только для отображения категорийных переменных, т.е.
величин, в которых важна не их величина, а порядок следования. Поэтому
линейные графики подходят для представления зависимостей от числа
главных компонент, например, для изображения того, как величины RMSEC и
RMSEP меняются при усложнении модели.

Методы построения  графиков в версиях 2003 и 2007 сильно
отличаются. Поэтому мы не будем на этом останавливаться, предоставив эту
тему для

самостоятельного изучения.