Как посчитать проценты от числа: формула и примеры

Как посчитать проценты, разделив число на 10

Сначала вы находите размер 10%, а потом делите или умножаете его, чтобы получить нужное количество процентов.

Пример

Допустим, вы кладёте на 530 тысяч рублей на 12 месяцев. Процентная ставка составляет 5%, капитализации не предусмотрено. Вы хотите узнать, сколько денег заберёте через год.

В первую очередь надо вычислить 10% от суммы. Разделите её на 10, передвинув запятую влево на один знак. Вы получите 53 тысячи.

Чтобы узнать, сколько составляют 5%, разделите результат на 2. Это 26,5 тысячи.

Если бы в примере речь шла о 30%, нужно было бы умножить 53 на 3. Для расчёта 25% пришлось бы умножить 53 на 2 и прибавить 26,5.

В любом случае такими крупными числами оперировать довольно просто.

Понятие процента и процентного соотношения

Процент представляет собой число или отношение, выраженное в виде доли от 100. Таким образом, 20% означает 20/100. Процент является одним из самых простых инструментов для сравнения данных, так как помогает сравнивать различные дроби, особенно в случаях дробей с различными знаменателями.

Под процентом мы подразумеваем, что это сотые доли от целого. Таким образом, х процентов означает х сотых, записанных как х%.

Чтобы выразить x% как дробь, мы имеем x% = x / 100.

Таким образом, 20% = 20/100 = 1/5.

Чтобы выразить a / b в процентах, мы имеем, a / b = (a / b) * 100%.

Таким образом, 1/4 = (1/4) * 100% = 25%.

Способы подсчета задач на проценты

1. Если A на R% больше, чем B, то B меньше, чем A на R / (100 + R) * 100
2. Если A на R% меньше, чем B, то B больше, чем A на R / (100- R) * 100
3. Если цена товара увеличивается на R%, то: R / (100 + R) * 100
4. Если цена товара уменьшается на R%, то: р / (100-р) * 100

Расчеты роста или снижения населения

Пусть население города сейчас будет P и предположим, что оно увеличивается со скоростью R% в год;

1. Население после n лет = P (1+ (R / 100))
2. Население n лет назад = P / (1+ (R / 100))
3. Если население увеличивается на x% в течение первого года, на y% в течение второго года, на z% в течение третьего года, население через три года будет:

P (1 + x / 100) ( 1 + у / 100) (1 + Z / 100)

Прогрессия в тестах на проценты

1. Если число увеличивается на х%, а затем уменьшается на х%, то число будет уменьшено на х2/100 процентов
2. Если число уменьшается на х%, и затем увеличилось на х% , то число будет уменьшено на х2/100 процентов
3. Если на экзамене, в котором минимальный процент прохождения составляет x%, кандидат получает оценку y и падает на z баллов, то общее количество баллов в этом экзамене будет 100 * (y + z) / x
4. Если на экзамене x% и y% кандидатов соответственно, потерпели неудачу в двух разных предметах, а z% кандидатов не сдавали оба предмета, то процент кандидатов, сдавших оба предмета, будет равен %

Расчеты цен, прибыли или убытка

1. Если цена продукта увеличивается или уменьшается на x%, а другой фактор уменьшается на y%, то результат определяется как:

[x + y + xy / 100]%

1. Если результат равен нулю, т. е. нет ни потерь ни прибыли, тогда приведенная выше формула имеет вид:

y = 100x / 100 + x

1. Если цена товара последовательно увеличивается на x%, y% и z%, то конечное увеличение цены составит:

[x + y + z + {xy + yz + zx} / (100) + xyz / 1002]%

1. Если после расходования сначала p1%, затем p2% от остатка и т. д., B — это сумма баланса, то общая (исходная) сумма определяется как:

Общая сумма = B * 100 * 100 ….. / (100-р2) …..

Читайте нашу отдельную статью Числовые тесты на расчет прибыли и убытка

Что означает процент

В переводе с латыни процент (per centum) означает «на сотню» или «сотая», то есть одна сотая доля числа. Принято обозначение знаком «%». Процент принято использовать, когда хотят указать точную долю чего-либо к одной единице. 100% — 1, соответственно, 25% — это 0,25 и 25/100.

Также с помощью этого понятия можно сравнивать разные величины, предварительно указывая, из какого целого нужно вычесть проценты. Скажем, доход больше расхода на 25%, стоимость авиабилетов снизилась на 3%, если сравнить с прошлогодними расценками, книга «Орден феникса» на 35% толще, чем «Кубок огня» и так далее. Бывает ситуация, когда процент получается больше 100, это значит, что доля вышла больше 1.

В финансах процент является оплатой заемщика кредитору за деньги, полученные на время. Процентщик — это человек, выдающий деньги на время под определённый процент. Человек, который брал кредит, в дальнейшем будет вынужден вернуть изначально взятую сумму, да ещё и доплатить сверху.

В бизнесе существует определение «работа за проценты», в таком случае размер заработной платы напрямую зависит от прибыли или оборота. Этот принцип несёт в себе как позитивные возможности, так и определенный риск, ведь с одной стороны можно заработать много, а можно не заработать ничего. Без процентов невозможно представить функционирования не только бизнеса, но и банков с бухгалтерией.

Формулы

Приведем пример существующих формул:

• В = А х Р : 100%; А = В х 100% : Р;
• Р = В : А х 100%; В = А х (1 + Р : 100%);
• В = А х (1 — Р : 100%);
• А = (В х 100%) : (100% + Р).

Также список продолжают формулы:

• А = (В х 100%) : (100% — Р);
• В = А х (1 + Р : 100%) х n.

Обозначения: В – будущая стоимость; А – текущая стоимость; Р – процентная ставка за определенный период; n – количество всех вычислительных периодов.

Приведем пример. Задача № 1: необходимо найти В, которое составляет 6% от 36. Решение: В = 36 х 6 : 100 = 2,16. Ответ: В = 2,16.

Задача № 2. Сколько процентов составляет число 37 от 21? Решение: 37 : 21 х 100 = 176%. Ответ: 176%.

Задача № 3. Найдем число на 17% меньше, чем 30. Решение: 30 х (1 — 17 : 100%) = 30 х 0,83 = 24,9. Ответ: число 24,9 меньше на 17% от 30.

На наглядном примере мы видим, что нет ничего сложного в решении задач с процентами. Главное, чтобы заранее был развит интерес к этой теме. И даже если отсутствуют знания, их можно восполнить, прочитав до конца эту статью.

Способ второй: переводим проценты в десятичную дробь

Как вы помните, процент — сотая часть числа. В виде десятичной дроби это 0,01 (ноль целых одна сотовая). Следовательно, 17% – это 0,17 (ноль целых, семнадцать сотых), 45% – 0,45 (ноль целых, сорок пять сотых) и т. д. Полученную десятичную дробь умножаем на сумму, процент от которой считаем. И находим искомый ответ.

Например, давайте рассчитаем сумму подоходного налога от зарплаты 35 000 рублей. Налог составляет 13%. В виде десятичной дроби это будет 0,13 (ноль целых, тринадцать сотых). Умножим сумму 35 000 на 0,13. Получится 4 550. Значит, после вычета подоходного налога вам будет перечислена зарплата 35 000 – 4 550 = 30 050. Иногда эту сумму уже без налога называют «зарплатой на руки» или «чистой». В противовес этому сумму вместе с налогом «грязной зарплатой». Именно «грязную зарплату» указывают в объявлениях о вакансиях компании и в трудовом договоре. На руки же даётся меньше. Сколько? Теперь вы легко посчитаете.

Расчет доли в процентах (удельного веса).

Давайте рассмотрим несколько примеров, которые помогут вам быстро вычислить долю в процентах от общей суммы в Excel для различных наборов данных.

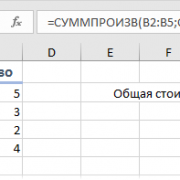
Пример 1. Сумма находится в конце таблицы в определенной ячейке.

Очень распространенный сценарий — это когда у вас есть итог в одной ячейке в конце таблицы. В этом случае формула будет аналогична той, которую мы только что обсудили. С той лишь разницей, что ссылка на ячейку в знаменателе является абсолютной ссылкой (со знаком $). Знак доллара фиксирует ссылку на итоговую ячейку, чтобы она не менялась при копировании формулы по столбцу.

Возьмем данные о продажах шоколада и рассчитаем долю (процент) каждого покупателя в общем итоге продаж. Мы можем использовать следующую формулу для вычисления процентов от общей суммы: 

=G2/$G$13

Вы используете относительную ссылку на ячейку для ячейки G2, потому что хотите, чтобы она изменилась при копировании формулы в другие ячейки столбца G. Но вы вводите $G$13 как абсолютную ссылку, потому что вы хотите оставить знаменатель фиксированным на G13, когда будете копировать формулу до строки 12.

Совет. Чтобы сделать знаменатель абсолютной ссылкой, либо введите знак доллара ($) вручную, либо щелкните ссылку на ячейку в строке формул и нажмите F4.

На скриншоте ниже показаны результаты, возвращаемые формулой. Столбец «Процент к итогу» отформатирован с применением процентного формата.

Пример 2. Часть итоговой суммы находится в нескольких строках.

В приведенном выше примере предположим, что у вас в таблице есть несколько записей для одного и того же товара, и вы хотите знать, какая часть общей суммы приходится на все заказы этого конкретного товара.

В этом случае вы можете использовать функцию СУММЕСЛИ, чтобы сначала сложить все числа, относящиеся к данному товару, а затем разделить это число на общую сумму заказов:

Учитывая, что столбец D содержит все наименования товаров, столбец F перечисляет соответствующие суммы, ячейка I1 содержит наименование, которое нас интересует, а общая сумма находится в ячейке F13, ваш расчет может выглядеть примерно так:

Естественно, вы можете указать название товара прямо в формуле, например:

Но это не совсем правильно, поскольку эту формулу придется часто корректировать. А это затратно по времени и чревато ошибками.

Если вы хотите узнать, какую часть общей суммы составляют несколько различных товаров, сложите результаты, возвращаемые несколькими функциями СУММЕСЛИ, а затем разделите это число на итоговую сумму. Например, по следующей формуле рассчитывается доля черного и супер черного шоколада:

Естественно, текстовые наименования товаров лучше заменить ссылками на соответствующие ячейки.

Для получения дополнительной информации о функции суммирования по условию ознакомьтесь со следующими руководствами:

• Как использовать функцию СУММЕСЛИ в Excel
• СУММЕСЛИМН и СУММЕСЛИ в Excel с несколькими критериями

Как посчитать проценты с помощью онлайн-сервисов

На сайте собраны разные калькуляторы, которые высчитывают не только проценты. Здесь есть сервисы для кредиторов, инвесторов, предпринимателей и всех тех, кто не любит считать в уме.

Самый простой и наглядный метод заключается в составлении пропорции. На ее основе происходят все дальнейшие вычисления. Выглядит это следующим образом:

• 45 – известное число, равное 100%.
• ? – число, которое составляет 15% от 45.

Далее, происходит упрощение дроби к уравнению с одной неизвестной. Согласно математическим законам, перекрестные данные в пропорциях равны между собой, то есть: 45*15%=?*100%. Для нахождения «?», пользуемся простым правилом и получаем следующее.

Расчет формулы пропорции всегда происходит по принципу умножения известных данных, стоящих по диагонали и разделением их на третье число.

Можно составить формулу с любым неизвестным в . Что б не путаться, проценты или число получается в результате, вспоминаем правило сокращения в дроби – если знак процента (%) или денежного обозначения (руб) присутствует и сверху и снизу, он сокращается. Пример:

В результате вычисления получается денежная сумма.

VII. Список литературы.

1. Виленкин Н.Я. Математика. Учебник для 5 класса средней школы. – М.: Просвещение, 2005.
2. Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б. Изучение процентов в основной школе //Математика в школе, 2002, №1.
3. Виленкин Н.Я. Математика. Учебник для 6 класса средней школы. – М.: Просвещение, 2005.
4. Белоусов Р.С. и др. Я познаю мир. Экономика. Энциклопедия. Москва ООО издательства АСТ, 2001 – 489с.
5. Липсиц И.В. Экономика М.: Вита – Пресс, 1996 – 352с.
6. Ресурсы интернет: ru.wikipedia.org
7. Барабанов О.О. Задачи на проценты как проблема нормы словоупотребления // Математика в школе, 2003 , №5.
8. Симонов А.С. Проценты и банковские расчеты //Математика в школе, 1998, № 4.
9. Симонов А.С. Сложные проценты //Математика в школе, 1998, № 5.
10. Дорофеев Г.В., Седова Е.А. Процентные вычисления. – Москва: Дрофа, 2003г.
11. Гончарова Л.В. Предметные недели в школе. Математика. Волгоград: издательство “Учитель”, 2003г.

Работу выполнил:
Большаков Антон
Ученик 6 “А” класса

Научный руководитель:
Макарова Галина Сергеевна
Учитель математики

Муниципальное бюджетное образовательное учреждение
“Школа № 128”
Нижний Новгород
2016 г.

Презентация: http://static.livescience.ru/percents/presentation.pptx

Частые задачи

Решение : Пользуемся первым калькулятором. Вводим в первое поле ставку 6, в второе 100000 Получаем 6000 руб. — сумма налога.

Задача 2. У Миши 30 яблок. 6 он отдал Кате. Сколько процентов от общего числа яблок Миша отдал Кате?

Решение: Пользуемся вторым калькулятором — в первое поле вводим 6, во второе 30. Получаем 20%.

Задача 3. У банка Тинькофф за пополнение вклада из другого банка вкладчик получает 1% сверху от суммы пополнения. Коля пополнил вклад переводом из другого банка на сумму 30 000. На какую итоговую сумму будет пополнен вклад Коли.

Решение : пользуемся 3м калькулятором. Вводим 1 в первое поле, 10000 во второе. Жмём расчёт получаем сумму 10100 руб.

Возможно, математика не была вашим любимым предметом в школе, а числа пугали и наводили тоску. Но во взрослой жизни от них никуда не деться. Без вычислений не заполнить квитанцию об оплате электроэнергии, не составить бизнес-проект, не помочь ребёнку с домашним заданием. Часто в этих и других случаях требуется посчитать процент от суммы. Как это сделать, если о том, что такое процент, со школьных времён остались смутные воспоминания? Давайте напряжём память и разберёмся.

Способ третий: считаем на калькуляторе

Если сомневаетесь в своих математических способностях, то воспользуйтесь калькулятором. С его помощью считается быстрее и точнее, особенно если речь идёт о больших суммах. Проще работать с калькулятором, у которого есть кнопка со знаком процент %. Сумму умножаем на количество процентов и нажимаем кнопку %. На экране высветится необходимый ответ.

Например, вы хотите посчитать, каким будет ваше пособие по уходу за ребёнком до 1,5 лет. Оно составляет 40% от среднего заработка за два последних закрытых календарных года. Допустим, средняя зарплата получилась 30 000 рублей. На калькуляторе 30 000 умножаем на 40 и нажимаем кнопку %. Клавишу = трогать не нужно. На экране высветится ответ 12 000. Это и будет величина пособия.

Как видите, всё очень просто. Тем более, что приложение «Калькулятор» сейчас есть в каждом сотовом телефоне. Если специальной кнопки % у аппарата нет, то воспользуйтесь одним из двух описанных выше способов. А умножение и деление произведите на калькуляторе, что облегчит и ускорит ваши вычисления.

Не забудьте: для облегчения подсчётов есть онлайн-калькуляторы. Действуют они так же, как и обычные, но всегда под рукой, когда вы работаете на компьютере.

Финансовые тесты на проценты для самостоятельных расчетов

Продавец получил прибыль, равную продажной цене 75 изделий, когда продал 100 изделий. Какую прибыль он получил от сделки?

• A) 33,33%
• B) 75%
• C) 300%
• D) 150%

Торговец покупает две партии товара за 600 рублей. Он продает одну из них с прибылью 22%, а другую — с убытком в 8% и в итоге не теряет прибыли. Какова цена продажи товара, который продается с убытком?

• А) 404.80 рублей
• В) 440 рублей
• С) 536,80 рублей
• D) 160 рублей

Продавец заявил, что продает свой товар с потерей в 8%, но весит он 900 граммов вместо веса в килограмм. Найдите его реальную потерю или прибыль.

1. A) 2% потерь
2. B) 2,22% прибыли
3. C) 2% прибыли
4. D) Ничего из этого

Роман продал товар за 56 рублей, а себестоимость товара Х рублей. Если он получил х% от своих расходов, какова была себестоимость?

• А) 40 рублей
• B) 45 рублей
• C) 36 рублей
• D) 28 рублей

Магазин покупает товар по сумме 19% от цены на этикетке. Если он хочет получить прибыль в размере 20% после предоставления суммы в 10%, на какой процент его цена должна превышать первоначальную цену на этикетке?

• A) + 8%
• B) -3,8%
• C) + 33,33%
• D) Ни один из них

Если яблоки покупаются из расчета 30 штук за рубль, то сколько яблок нужно продавать за рубль, чтобы получить 20% прибыли?

• A) 28
• B) 25
• C) 20
• D) 22

Два торговца продают каждый предмет за 1000 рублей. Если торговец A рассчитывает свою прибыль по себестоимости, а торговец B вычисляет свою прибыль по продажной цене, они получают прибыль в размере 25% соответственно. Насколько прибыль, полученная Торговцем B, больше, чем прибыль Торговца A?

• A) 66,67 рублей
• B) 50 рублей
• C) 125 рублей
• D) 200 рублей

Продавец продает свои товары таким образом, чтобы прибыль от продажи 50 товаров равнялась продажной цене 25 товаров. Какова его прибыль?

• A) 25%
• B) 50%
• C) 100%
• D) 66,67%

Торговец продает свой товар на 75% выше его себестоимости. Какую максимальную сумму в процентах он может предложить, чтобы он в конечном итоге продал без прибыли или убытка?

• A) 75%
• B) 46,67%
• C) 300%
• D) 42,85%

Ключи к ответам:

1.C;  2.A;  3.B;  4.A;  5.A;  6.B;  7.B;  7.B;  8.C;  9.D

Читайте больше о числовых тестах и методиках их быстрого решения в наших статьях:

Числовые тесты на проценты могут быть очень непростыми. Основная их сложность заключается даже не в самих расчетах, а в том, что их требуется решить за ограниченное время — обычно 60 секунд. Но нет ничего невозможного. За 3-4 дня практики на HRLider.ru вы увидите разные примеры числовых тестов и поймете, как их решать быстро и точно. Если вам предстоят числовые тесты, подготовьтесь — гарантируйте свой успех.

Как просчитать процент на калькуляторе

Затем в поля нужно ввести запрашиваемые данные и получить результат. При этом можно узнать, как % от общего числа, так и сколько процентов составляет значение одного числа от другого.Подводя итоги, можно сказать, что калькулятор позволяет определиться с такими вопросами:

1. Вычислить определенный % из определенного значения. Или, если известен %, то прибавить его к какому-то числу.
2. Какой % составляет от заданного показателя.
3. Сколько % содержит одно значение от другого.

На обычном калькуляторе также есть функция определения %. Если опция есть, то должна быть клавиша, где изображен %.

Для этого найдите на его клавиатуре кнопку с изображением процента (%).

Для этого проведем следующие манипуляции:

Введите 125 на калькуляторе. Нажмите умножить (*). Нажмите 12. Затем нажмите кнопку с процентом. При этом на экране отобразиться результат – 9,6%.

Таким образом, можно найти любые другие значения с двумя числами. Калькулятором можно и воспользоваться на мобильном телефоне.

В ноутбуке или компьютере полезную программку можно отыскать через меню пуск.

Онлайн-сервисы для вычислений

В нахождении нужных процентов могут помочь различные сервисы-калькуляторы, работающие в режиме онлайн. Например, популярный сайт fin-calc.org.ua имеет в своём функционале различные инструменты, помогающие, в том числе, высчитать процент от любого числа.

1. Перейдите на fin-calc.org.ua.
2. Введите искомые показатели в соответствующие клетки.
3. Нажмите на «Рассчитать». Вы сразу же получите искомый результат.

Калькуляционные вычисления на fin-calc.org.ua

Также указанный калькулятор позволяет высчитать какую долю от 1 составляет 2, прибавить % к числу или вычесть из него. Всё очень быстро и удобно.

Способы расчета

В учебнике математики за 5-ый класс можно узнать, что % составляет сотую часть от числа. Чтобы узнать, сколько % от определенного значения, можно воспользоваться пропорцией и составить правило креста.

Например, нужно найти 500 от 1000. При этом данные, которые располагаются напротив друг друга необходимо перемножить, а затем разделить на третье число.

При этом числа пишутся под цифрами, а проценты под такими же показателями.Получается:

Можно использовать и программу Excel.

Сначала создайте на рабочем столе лист Excel.

Затем откройте документ и в выделенной строке введите:

• = (равно);
• затем 8500;
• после этого нажмите * (умножить);
• затем 15;
• после следует нажать клавишу % и Enter.

Формулы простых и сложных процентов

Поскольку простые и сложные проценты чаще всего используются при расчете прибыли от банковских вкладов, продолжим на их примере. Для решения задач нам понадобится такая информация:

• К — начальная сумма вклада;
• К — конечная сумма вклада;
• R — ставка доходности, переводится из процентов в число (10% = 0.1);
• N — количество периодов (лет).

Формула простого процента

По этой формуле мы можем рассчитать конечную сумму вклада без капитализации полученной прибыли. Для этого нужно знать начальную сумму вклада, процентную ставку за 1 период инвестирования и временной интервал. Если конечная сумма задана сразу и нужно найти другую неизвестную переменную, используйте производные формулы простого процента:

Формула сложного процента

По этой формуле мы можем посчитать конечную сумму вклада с учётом капитализации полученной прибыли, зная начальный депозит, процентную ставку и нужный временной интервал. Для решения задач также можно использовать производные формулы сложного процента:

На практике часто дело не заканчивается первоначальным депозитом — многие пользуются регулярными пополнениями, например делают регулярные инвестиции из зарплаты. Для этих случаев формула сложного процента становится длиннее:

где D — сумма регулярных пополнений банковского депозита

Обратите внимание, степень N-1 означает, что доливки начинаются со второго инвестиционного периода (если сумма дополнительных инвестиций вносится сразу, то N-1 меняется на N)

Ну что, удачи на экзаменах всем читающим меня студентам 🙂 Для закрепления далее мы разберем несколько примеров задач на сложные проценты.

Как высчитать проценты при помощи соотношений

Иногда бывают ситуации, в которых быстрее всего будет пользоваться простыми дробями.

• 10% — это одна десятая часть, которую можно найти, если разделить число на 10.
• 12,5% — одна восьмая часть. Для этой информации число делить надо на 8.
• 20% — одна пятая часть.
• 25% — четверть.
• 50% — половина.
• 75% — три четверти. Делим известное число на 4, затем умножаем на 3.

В определенных ситуациях проще будет обратиться к простым дробям.

• 10%- это 1/10 числа, а значит, делим целое на 10.
• 12,5% — 1/8.
• 20% — 1/5.
• 25% — 1/4.
• 50% — 1/2.
• 75% — 3/4. Значит, снова делим на 4, а потом умножаем на 3.

Допустим, билет на самолет в Италию стоит 75 000 рублей, однако на него сейчас скидка 75%. Проблема в том, что вы сейчас можете себе позволить потратить лишь 20 000 рублей. Понять уложитесь ли вы, получится следующим образом:

• 100% — 75% = 25% — стоимость путешествия в процентах от изначальной цены после учета скидки.
• 75 000 / 4 = 18 750 рублей.

Расчет процентов в Excel.

Основная формула для расчета процента от числа в Excel такая же, как и во всех сферах жизни:

Часть / Целое = Процент

Если вы сравните ее с основной математической формулой для процента, которую мы указали чуть выше, то  заметите, что в формуле процента в Excel отсутствует часть * 100. При вычислении процента в Excel вам совершенно не обязательно умножать полученную дробь на 100, поскольку программа делает это автоматически, когда процентный формат применяется к ячейке.

И если в Экселе вы будете вводить формулу с процентами, то можно не переводить в уме проценты в десятичные дроби и не делить величину процента на 100. Просто укажите число со знаком %.

То есть, вместо =A1*0,25   или =A1*25/100 просто запишите формулу процентов  =A1*25%.

Хотя с точки зрения математики все 3 варианта возможны и все они дадут верный результат.

А теперь давайте посмотрим, как можно использовать формулу процента в Excel для реальных данных. Предположим, в вашей таблице Эксель записана сумма заказанных товаров в столбце F и оставленных товаров в столбце G. Чтобы высчитать процент доставленных товаров, выполните следующие действия:

• Введите формулу =G2/F2 в ячейку H2 и скопируйте ее на столько строк вниз, сколько вам нужно.
• Нажмите кнопку «Процентный стиль» ( меню «Главная» > группа «Число»), чтобы отобразить полученные десятичные дроби в виде процентов.
• Не забудьте при необходимости увеличить количество десятичных знаков в полученном результате.
• Готово! 🙂

Такая же последовательность шагов должна быть выполнена при использовании любой другой формулы процентов в Excel.

На скриншоте ниже вы видите округленный процент доставленных товаров без десятичных знаков.

Чтобы определить процент доставки, мы сумму доставленных товаров делим на сумму заказов. И используем в ячейке процентный формат, при необходимости показываем десятичные знаки.

Запишите формулу в самую верхнюю ячейку столбца с расчетами, а затем протащите маркер автозаполнения вниз по столбцу. Таким образом, мы посчитали процент во всём столбце.

История возникновения процентных задач

Латинское выражение pro centum определяется как «за сотню», «со ста». Но произошло оно от итальянского слова, которое пишется как «сто». Однако еще существует предположение, что знак «%» (процент) появился через оплошность писателя книги. Он вместо «сто» напечатал %. Один инженер из Нидерландов как первооткрыватель выпустил в мир процентную таблицу расчетов в 1584 г. Сначала эта наука применялась в торговых областях, затем постепенно проценты стали использовать в технических работах, науке, хозяйственных делах, статистике. Можно сделать вывод, что математика и использование процентных вычислений очень пригодятся в жизни.

Как посчитать проценты от числа

Есть несколько способов провести эти математические исчисления, и один из них, конечно же, калькулятор. Но мы не будем идти по пути наименьшего сопротивления, а рассмотрим и другие приемы, как высчитать процент от числа.

Как посчитать проценты методом деления на 100

Поскольку процент – это и есть сотая часть, то чтобы узнать величину одного процента, достаточно разделить само число на 100. А уже дальше находить необходимое число процентов, умножая их на величину 1%. Например, 1% от 500 – это 5. Вам необходимо узнать, сколько составят 20%. 20 умножаем на 5 и получаем 100. Такой способ удобен для целых чисел, а вот с дробными придется пораскинуть мозгами.

Как вычислить проценты методом деления на 10

Такой способ практически не отличается от деления на 100, но только применять его лучше для вычисления процентов, кратных пяти (5, 10, 15, 20 и т.д.). 

Вам нужно вычислить 30 процентов от числа 8900. Для этого сначала 8900 делим на десять (тут достаточно отнять последний ноль), а затем, чтобы найти процент от числа, результат умножаем на 3. 8900/10=890, 890*3= 2670. Это и есть нужное вам число. 

Как вычислить проценты через составление пропорций

Хорошая новость – этим методом можно вычислить проценты от любого числа, плохая – придется вспоминать школьную программу. Пропорция – это это равенство двух отношения, проще говоря, когда a так относится к b, как c к d. На примере формулы выглядит так: a:b=c:d, или же, в нашем случае, вся сумма (100%) : 100% = часть суммы : искомое число процентов. Не пугайтесь, на «живых» числах расчет процентов выглядит проще. Пускай, ваша сумма равна 280, а ее часть – 70, и нужно определить, сколько процентов составляет 70. Для этого записываем пропорцию: 280:100=70:Х, где икс – искомая нами процентная доля. 

Х=70х100:280, Х=25. То есть, 70 – это 25% от 280.

Вычисляем проценты с помощью соотношений

Иногда для расчетов удобно пользоваться методом простых дробей. Например, если целое число – это 100 %, то 10% – 1/10 числа. А чтобы узнать процентное соотношение в цифрах, нужно просто разделить сумму на 10. С другими процентами несколько сложнее:

• 20% – это 1/5, то есть нужно делить число на 5;
• 25% – 1/4 (делим на 4);
• 50% – 1/2 (делим пополам);
• 12,5% – 1/8 (а здесь – на 8);
• 75% – это 3/4. То есть, сначала делим сумму на 4, а результат умножаем на 3.

Разберемся на примере. Вам нужно узнать процент от числа, допустим, получить 75 % от 5660. Для этого 5600 делим на 4, получаем 1415. А уже это число умножаем на 3. 4245 – это 75% от 5660. 

5660/4х3=4245.

Как посчитать проценты с калькулятором

Если все математические исчисления для вас хуже пытки, призовем на помощь технический прогресс. То есть, будем считать проценты при помощи калькулятора.

Делать это довольно просто:

• Чтобы посчитать процент от суммы, нужно ввести само число (100%), знак умножения, затем нужное нам число процентов и знак %. Для примера из второго способа это выглядит так: 8900 х 30%
• Чтобы узнать сумму, меньшую на определенный процент, нужно ввести число, знак минус, число процентов и знак %. Например,  256 – 8% = 235,52.
• Таким же методом прибавляются проценты к числу: 483+13% = 545,79.

Конечно, сейчас существуют и онлайн-калькуляторы, с помощью которых можно производить куда более сложные финансовые расчеты. А также вычислять калорийность продуктов, разные показатели красоты и здоровья, производить нужные в быту расчеты. Пользоваться ими при наличии интернета легко, но надеемся, что и наши способы считать проценты вам помогут.