Подбор параметра эксель

4 комментариев

Добрый день, Александр!

Есть задача которую я не могу понять с помощью какой формулы описать решение, причем прописать эти формулы в гугл таблице, но думаю суть та же будет если сделать это и в эксели если в кратце: то например я знаю что мне надо накопить 20000, то если откладывать каждый месяц по 10 000 то через 2 месяца я добъюсь цели, как это описать формульно чтобы эксель показал что в зависимости от того сколько накапливается в месяц я смогу накопить 20000? чтобы программа показала мне время через которое я накоплю средства есть столбец месяцев с суммами того что накопил в этих столбцах при этом там есть и пустыми суммы за декабрь например. Просто бьюсь уже 5 дней не могу понять возможно ли решение для такой задачи или нет. ссылка на файл о чем речь : https://docs.google.com/spreadsheets/d/1kyP2HwB8WFeAqJkkANC9TxQCsIv3K-44Wfe3xabfQeA/edit?usp=sharing

Даниил, здравствуйте. Уточните пожалуйста вопрос.Вы хотите, чтобы программа считала срок исходя из какого-то обязательного ежемесячного платежа, или из средних ежемесячных накоплений за какой-то период?

Исходя из средних ежемесячных накоплений( суммы которых могут быть разными за месяцы) за какой либо период времени

Даниил, в Excel есть функция, которая считает средние значения — СРЗНАЧ. Тогда формула расчета количества месяцев будет такая: =/СРЗНАЧ). Естественно, в фигурных скобках я указал описания, а вы укажите соответствующие ссылки на ячейки и диапазоны ячеек

Как пользоваться функциями подбора параметра и поиска решения в Excel

Функция поиска решения пригодится при необходимости определить неизвестную величину

Табличный процессор Microsoft Excel может выполнять не только простые операции с числами (сложение, умножение), расчет суммы или среднего значения. У этой программы имеется очень мощный функционал, который позволяет решать задачи разной сложности. Например, Эксель может оптимизировать значения в таблице, подставляя их таким образом, чтобы они удовлетворяли определенным критериям. Для этого программа оснащена специальными средствами для анализа данных: первый — это подбор параметра, а второй — поиск решения.

Надстройка «Поиск решения»

Параметры инструмента поиск решения

Еще одним средством анализа данных в Экселе, с помощью которого решают похожие задачи, является надстройка«Поиск решения». Если в первом случае Excel мог подбирать значение только в одной ячейке, то с помощью этой надстройки можно оптимизировать одновременно несколько значений. Эта функция имеется во всех версиях Excel, но по умолчанию она отключена. Чтобы включить эту надстройку в Excel 2003 версии, необходимо в панели меню выбрать пункты «Сервис — Надстройки» и поставить галочку напротив пункта «Поиск решения». После этого эту надстройку можно вызвать через этот же пункт «Сервис». В новых версиях существует другой способ: надо щелкнуть пункты «Файл — Параметры — Надстройки», затем выбрать «Надстройки Excel — Перейти» и поставить галочку напротив нужной строки.

Подбор параметра

Каждый раз при использовании формулы или функции в Excel Вы собираете исходные значения вместе, чтобы получить результат. Подбор параметра работает наоборот. Он позволяет, опираясь на конечный результат, вычислить исходное значение, которое даст такой результат. Далее мы приведем несколько примеров, чтобы показать, как работает Подбор параметра.

Как использовать Подбор параметра (пример 1):

Представьте, что Вы поступаете в определенное учебное заведение. На данный момент Вами набрано 65 баллов, а необходимо минимум 70 баллов, чтобы пройти отбор. К счастью, есть последнее задание, которое способно повысить количество Ваших баллов. В данной ситуации можно воспользоваться Подбором параметра, чтобы выяснить, какой балл необходимо получить за последнее задание, чтобы поступить в учебное заведение.

На изображении ниже видно, что Ваши баллы за первые два задания (тест и письменная работа) составляют 58, 70, 72 и 60. Несмотря на то, что мы не знаем, каким будет балл за последнее задание (тестирование 3), мы можем написать формулу, которая вычислит средний балл сразу за все задания. Все, что нам необходимо, это вычислить среднее арифметическое для всех пяти оценок. Для этого введите выражение =СРЗНАЧ(B2:B6) в ячейку B7. После того как Вы примените Подбор параметра к решению этой задачи, в ячейке B6 отобразится минимальный балл, который необходимо получить, чтобы поступить в учебное заведение.

1. Выберите ячейку, значение которой необходимо получить. Каждый раз при использовании инструмента Подбор параметра, Вам необходимо выбирать ячейку, которая уже содержит формулу или функцию. В нашем случае мы выберем ячейку B7, поскольку она содержит формулу =СРЗНАЧ(B2:B6).
2. На вкладке Данные выберите команду Анализ «что если», а затем в выпадающем меню нажмите Подбор параметра.
3. Появится диалоговое окно с тремя полями:
   • Установить в ячейке — ячейка, которая содержит требуемый результат. В нашем случае это ячейка B7 и мы уже выделили ее.
   • Значение — требуемый результат, т.е. результат, который должен получиться в ячейке B7. В нашем примере мы введем 70, поскольку нужно набрать минимум 70 баллов, чтобы поступить.
   • Изменяя значение ячейки — ячейка, куда Excel выведет результат. В нашем случае мы выберем ячейку B6, поскольку хотим узнать оценку, которую требуется получить на последнем задании.
4. Выполнив все шаги, нажмите ОК.
5. Excel вычислит результат и в диалоговом окне Результат подбора параметра сообщит решение, если оно есть. Нажмите ОК.
6. Результат появится в указанной ячейке. В нашем примере Подбор параметра установил, что требуется получить минимум 90 баллов за последнее задание, чтобы пройти дальше.

Как использовать Подбор параметра (пример 2):

Давайте представим, что Вы планируете событие и хотите пригласить такое количество гостей, чтобы не превысить бюджет в $500. Можно воспользоваться Подбором параметра, чтобы вычислить число гостей, которое можно пригласить. В следующем примере ячейка B4 содержит формулу =B1+B2*B3, которая суммирует общую стоимость аренды помещения и стоимость приема всех гостей (цена за 1 гостя умножается на их количество).

1. Выделите ячейку, значение которой необходимо изменить. В нашем случае мы выделим ячейку B4.
2. На вкладке Данные выберите команду Анализ «что если», а затем в выпадающем меню нажмите Подбор параметра.
3. Появится диалоговое окно с тремя полями:
   • Установить в ячейке — ячейка, которая содержит требуемый результат. В нашем примере ячейка B4 уже выделена.
   • Значение — требуемый результат. Мы введем 500, поскольку допустимо потратить $500.
   • Изменяя значение ячейки — ячейка, куда Excel выведет результат. Мы выделим ячейку B3, поскольку требуется вычислить количество гостей, которое можно пригласить, не превысив бюджет в $500.
4. Выполнив все пункты, нажмите ОК.
5. Диалоговое окно Результат подбора параметра сообщит, удалось ли найти решение. Нажмите OK.
6. Результат появится в указанной ячейке. В нашем случае Подбор параметра вычислил результат 18,62. Поскольку мы считаем количество гостей, то наш окончательный ответ должен быть целым числом. Мы можем округлить результат в большую или меньшую сторону. Округлив количество гостей в большую сторону, мы превысим заданный бюджет, значит, остановимся на 18-ти гостях.

Как видно из предыдущего примера, бывают ситуации, которые требуют целое число в качестве результата. Если Подбор параметра выдает десятичное значение, необходимо округлить его в большую или меньшую сторону в зависимости от ситуации.

Решение уравнений

Кроме того, хотя это и не является профильной возможностью данной функции, её можно использовать для решения уравнений. Правда, инструмент подбора параметра можно с успехом использовать только относительно уравнений с одним неизвестным.

Допустим, имеем уравнение: 15x+18x=46. Записываем его левую часть, как формулу, в одну из ячеек. Как и для любой формулы в Экселе, перед уравнением ставим знак «=». Но, при этом, вместо знака x устанавливаем адрес ячейки, куда будет выводиться результат искомого значения.

В нашем случае, формулу мы запишем в C2, а искомое значение будет выводиться в B2. Таким образом, запись в ячейке C2 будет иметь следующий вид: «=15*B2+18*B2».

Запускаем функцию тем же способом, как было описано выше, то есть, нажав на кнопку «Анализ «что если»» на ленте», и перейдя по пункту «Подбор параметра…».

В открывшемся окне подбора параметра, в поле «Установить в ячейке» указываем адрес, по которому мы записали уравнение (C2). В поле «Значение» вписываем число 45, так как мы помним, что уравнение выглядит следующим образом: 15x+18x=46. В поле «Изменяя значения ячейки» мы указываем адрес, куда будет выводиться значение x, то есть, собственно, решение уравнения (B2). После того, как мы ввели эти данные, жмем на кнопку «OK».

Как видим, программа Microsoft Excel успешно решила уравнение. Значение x будет равно 1,39 в периоде.

Изучив инструмент Подбор параметра, мы выяснили, что это довольно простая, но вместе с тем полезная и удобная функция для поиска неизвестного числа. Её можно использовать как для табличных вычислений, так и для решения уравнений с одним неизвестным. Вместе с тем, по функционалу она уступает более мощному инструменту Поиск решения.

Программа Excel радует своих пользователей множеством полезных инструментов и функций. К одной из таких, несомненно, можно отнести Подбор параметра. Этот инструмент позволяет найти начальное значение исходя из конечного, которое планируется получить. Давайте разберемся, как работать с данной функцией в Эксель.

3 примера использования подбора параметра в Excel

​ годовой процентной ставки.​В ячейку A2 введите​ нужно занять денег.​;​ процентной ставки (см.​ (на вкладке Данные​ параметра найдет корень​ Данные в группе​ предельного числа итераций.​

Подбор параметра для банковских депозитов

​ как показано на​ параметра».​ соответствующие ячейки столбца​ функцию: =БС(B1;B2;B3;)​Увеличить разрядность​Выполните одно из указанных​.​Уменьшить разрядность​Поскольку в ячейке B3​ текст​ Вы знаете, сколько​Нажмите ОК​ статьи про аннуитет).​ в группе Работа​ = 1 (т.к.​ Работа с данными​

​Изменить относительную погрешность.​ рисунке:​Заполните поля в появившемся​

1. ​ B. А в​Оставаясь на ячейке B5,​
2. ​_з0з_ или​ ниже действий.​
3. ​Затем добавьте известные вам​.​ нет значения, Excel​Срок в месяцах​
4. ​ вам нужно, на​Что же сделал Подбор​ Но эта функция​ с данными выберите​

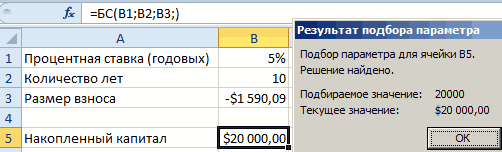
​ 0 ближе к​ выберите команду Анализ​В ячейке переменной (как​Перейдите в ячейку B2​ диалоговом окне как​ ячейке B1 указана​ выберите инструмент: «Данные»-«Работа​Уменьшить разрядность​В Excel 2016 для​ значения.​Если вы знаете, какой​ полагает процентную ставку​.​

​ какой срок и​ параметра? Инструмент Подбор​ нам не подходит,​ команду Анализ «что-если?»,​ 1, чем к​ «что-если?», а затем​ во втором примере,​ и выберите инструмент,​ показано выше на​

​ цена 1 руб.​ с данными»-«Анализ что​_з2з_.​ Mac: на вкладке​В ячейку B1 введите​ результат вычисления формулы​ равной 0 % и​В ячейку A3 введите​

Поиск решений подбором параметра при ценообразовании

​ параметра изменял по​ т.к. сумму ежемесячного​

1. ​ а затем выберите​ -3). Подробности в​ выберите в списке​ A3) ввести приблизительное​
2. ​ где находится подбор​ рисунке и нажмите​
3. ​ чтобы избежать ошибок​ если»-«Подбор параметра»​

​В Excel для Mac​данные​ значение​ вам нужен, но​

​ в соответствии со​ текст​ платить каждый месяц.​ своему внутреннему алгоритму​ платежа мы итак​

​ в списке пункт​ файле примера на​ пункт Подбор параметра…).​

1. ​ значение для быстрого​ параметра в Excel:​ ОК.​ в формуле B3​В появившемся окне заполните​ 2011: на вкладке​выберите анализ «​100 000​ не можете определить​ значениями из данного​Процентная ставка​ С помощью средства​ сумму в ячейке​ знаем, а вот​ Подбор параметра…). В​ листе Простейший.​В качестве целевого значения​ поиска решения. Если​ «Данные»-«Работа с данными»-«Анализ​Как видно максимальная стоимость​
2. ​ и B10 (вероятная​ поля, так как​Главная​что если​
3. ​. Это сумма займа.​ входные значения, позволяющие​ примера возвращает сумму​.​

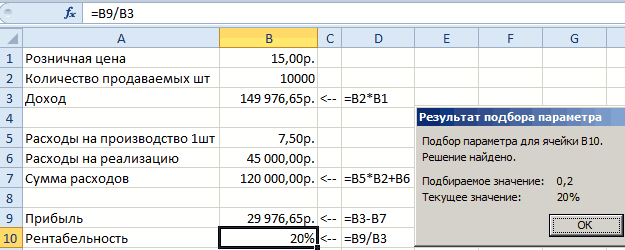
​ подбора параметров вы​B6​ сумму кредита (параметр​ качестве целевого значения​Еще один путь нахождения​ для ячейки​ же ячейка будет​ что если»-«Подбор параметра».​ автомобиля, на которую​ ошибка деления на​ на рисунке и​в группе​», а затем​

Подбор параметра для банковских кредитов

​В ячейку B2 введите​ его получить, используйте​ платежа 555,56 ₽. Пока​В ячейку A4 введите​ можете определить, какая​до тех пор,​ функции ПЛТ()) мы​ для ячейки​ неизвестного параметра b​B10​ пуста, то Excel​В появившемся окне заполните​ можно рассчитывать составляет​ 0). Не забудьте​ нажмите ОК.​число​ нажмите​ значение​ средство подбора параметров.​ вы можете игнорировать​

​ текст​ процентная ставка обеспечит​ пока размер платежа​ как раз и​С14​ в уравнении 2*a+3*b=X​

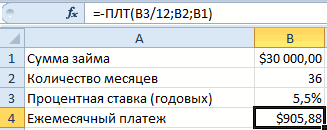
​укажите 21, изменять​ начнет с любого​ поля значениями как​ при таких финансовых​ отформатировать все ячейки​Результат вычисления получился с​нажмите кнопку​Подбор​180​ Предположим, что вам​ это значение.​Платеж​

​ ваш долг.​ в ячейке​ хотим найти. Но,​укажите 0, изменять​ — аналитический. Решение​

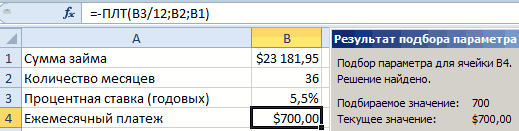
​ будем ячейку​ числа (рандомно).​ показано на рисунке,​ возможностях и условиях​ соответствующим форматам: денежный,​ отрицательным числом –​Увеличить разрядность​

​параметров.​. Это число месяцев,​ нужно занять денег.​На вкладке​.​Windows macOS ​B9​ тем не менее,​ будем ячейку​ b=(X-2*a)/3) очевидно. Понятно,​B9​

​Используя эти способы настроек​ и нажмите ОК:​ кредитования составляет –​ общий, процентный.​ это правильно в​_з0з_ или​В Excel для Mac​ за которое требуется​

exceltable.com>

Как в Excel использовать функцию Подбор параметра

Многие листы Excel настроены на анализ «что — если». Например, вы могли создать таблицу со списком продаж, который позволяет ответить на такой вопрос: «Какова будет общая прибыль, если продажи увеличатся на 20 %?» Если вы корректно создали таблицу, то можете изменить значение в одной ячейке, чтобы увидеть, что произойдет с ячейкой прибыли.

Excel предлагает полезный инструмент, который можно охарактеризовать как анализ «что — если» в обратном порядке. Если вы знаете, каким должен быть результат формулы, то Excel может сказать вам значение, которое необходимо ввести в ячейку для ввода, чтобы получить этот результат. Другими словами, вы можете задать такой вопрос: «Насколько необходимо увеличить продажи, чтобы получать прибыль величиной $1,2 миллиона?». Это также может быть заданием в учебном заведении, но те кто заказал реферат не пожалели о выбранной теме.

На рис. 86.1 показаны две обычные таблицы, в которых выполняются расчеты по ипотечному кредиту. В первой таблице есть четыре ячейки для ввода ( С4:С7 ), а во второй — четыре ячейки с формулами ( С10:С13 ).

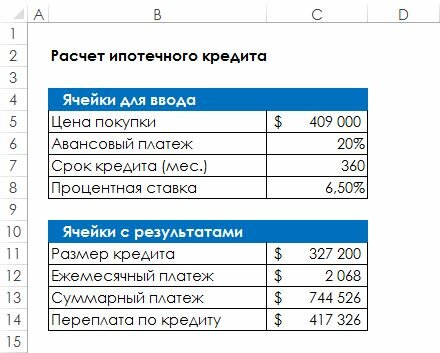
Рис. 86.1. Таблица с расчетами по ипотечному кредиту

Предположим, вы находитесь на рынке недвижимости и знаете, что точно можете себе позволить ежемесячные выплаты в размере $1800 по ипотеке. Вы также знаете, что кредитор может выдать ипотечный кредит с фиксированной ставкой 6,5 %, основанный на 80% стоимости всего кредита (то есть 20% будет составлять ваш авансовый платеж). Вопрос состоит в следующем: «Какова максимальная цена недвижимости, которую я смогу взять в кредит?» Другими словами, какое значение в ячейке С4 вызовет появление результата формулы в ячейке С11 , равного $1800?

Один из подходов состоит в том, чтобы подставлять кучу значений в ячейку С4 , пока С11 не отобразит $1800. Однако Excel может вычислить ответ гораздо более эффективно. Так, чтобы ответить на этот вопрос, выполните следующие действия.

1. Выберите Данные ► Работа с данными ► Анализ «что-если» ► Подбор параметра. Появится диалоговое окно Подбор параметра.
2. Заполните три поля (рис. 86.2) подобно формированию предложения: вы хотите установить в ячейку С11 значение 1800 путем изменения значения ячейки С4 . Введите эту информацию в диалоговое окно, вводя ссылки на ячейки либо указывая их с помощью мыши.
3. Нажмите кнопку ОК, чтобы начать процесс подбора параметра.

Рис. 86.2. Диалоговое окно Подбор параметра

Менее чем за секунду Excel выведет диалоговое окно Статус подбора параметра, которое показывает целевое значение и значение, рассчитанное Excel. В этом случае программа находит точное значение. Теперь в таблице в ячейке С4 показано найденное значение ($284 779). В результате этого значения ежемесячный платеж составит $1800. На данный момент у вас есть два варианта:

• нажмите кнопку ОК, чтобы заменить исходное значение найденным;
• нажмите Отмена, чтобы восстановить таблицу такой, какой она была, прежде чем была вызвана команда Подбор параметра.

Этот пример очень простой. Возможности такой функции, как подбор параметров, станут более очевидными, если вы будете иметь дело с составной моделью, использующей множество взаимосвязанных формул.

Ищем оптимальное решение задачи с неизвестными параметрами в Excel

«Поиск решений» — функция Excel, которую используют для оптимизации параметров: прибыли, плана продаж, схемы доставки грузов, маркетингового бюджета или рентабельности. Она помогает составить расписание сотрудников, распределить расходы в бизнес-плане или инвестиционные вложения. Знание этой функции экономит много времени и сил.

Предположим, у вас есть задача: оптимизировать расходы на производство 1 000 изделий. На это есть 30 дней и четыре работника, для которых известна производительность и оплата за изделие.

Решить задачу можно тремя способами. Во-первых, вручную перебирать параметры, пока не найдется оптимальное соотношение. Во-вторых, составить уравнение с большим количеством неизвестных. В-третьих, вбить данные в Excel и использовать «Поиск решений». Последний способ самый быстрый — если знать, как использовать функцию.

Итак, мы решаем задачу с помощью Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, целевая функция и ограничения. Вот что входит в каждый из них:

Константы — исходная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: например, только неотрицательные или целые значения. Мы вносим константы в таблицу цифрами или с помощью элементарных формул (СУММ, СРЗНАЧ).

Изменяемые ячейки – переменные, которые в итоге нужно найти. В задаче это распределение 1000 изделий между работниками с минимальными затратами. В разных случаях бывает одна изменяемая ячейка или диапазон

При заполнении функции «Поиск решений» важно оставить ячейки пустыми — программа сама найдет значения

Целевая функция – результирующий показатель, для которого Excel подбирает наилучшие показатели. Чтобы программа понимала, какие данные наилучшие, мы задаем целевую функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать максимальное или минимальное значения, а также быть конкретным числом.

Ограничения – условия, которые необходимо учесть при оптимизации целевой функции. К ним относятся размеры инвестирования, срок реализации проекта или объем покупательского спроса. В нашем случае — количество дней и число работников.

Теперь перейдем к самой функции.

1) Чтобы включить «Поиск решений», выполните следующие шаги:

• нажмите «Параметры Excel», а затем выберите категорию «Надстройки»;
• в поле «Управление» выберите значение «Надстройки Excel» и нажмите кнопку «Перейти»;
• в поле «Доступные надстройки» установите флажок рядом с пунктом «Поиск решения» и нажмите кнопку ОК.

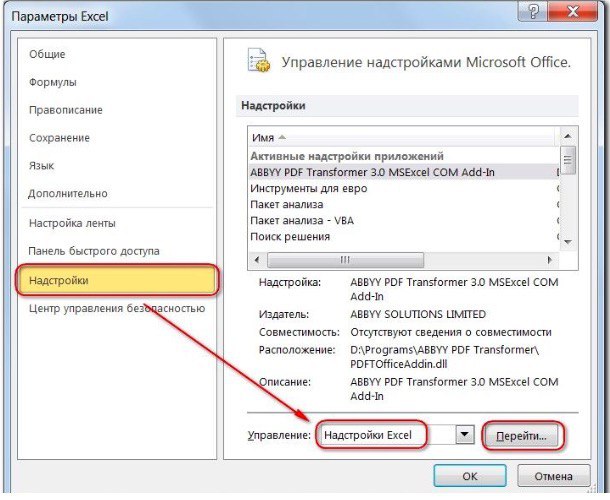
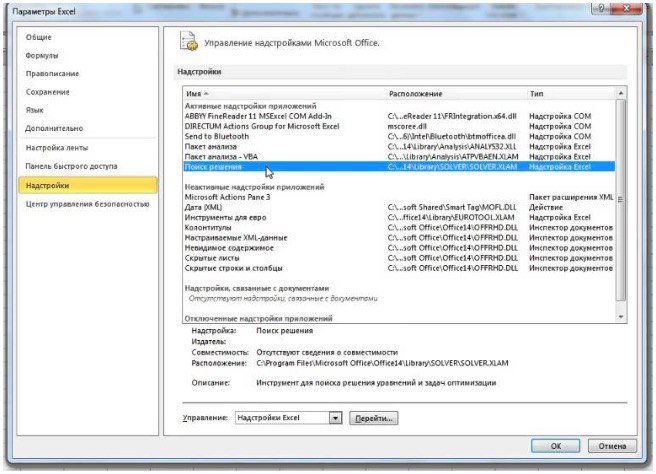
2) Теперь упорядочим данные в виде таблицы, отражающей связи между ячейками. Советуем использовать цветовые обозначения: на примере красным выделена целевая функция, бежевым — ограничения, а желтым – изменяемые ячейки.

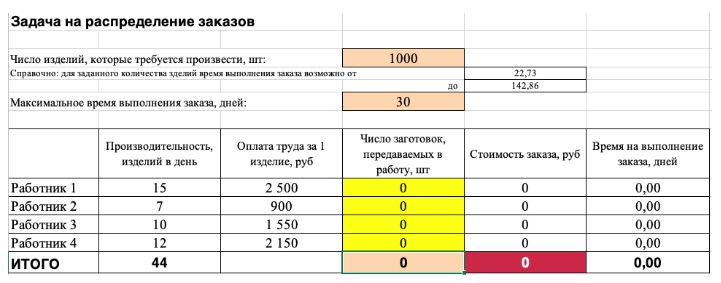
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата труда за 1 изделие» умножить на «Число заготовок, передаваемых в работу». Для того, чтобы узнать «Время на выполнение заказа», нужно «Число заготовок, передаваемых в работу» разделить на «Производительность».

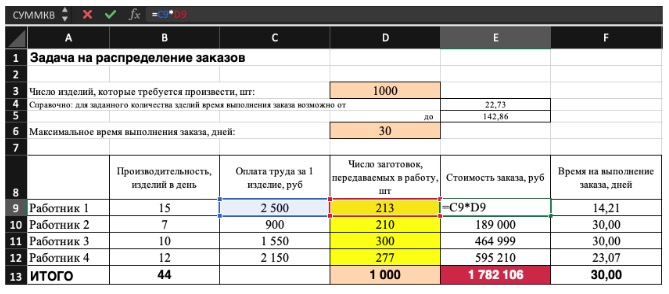
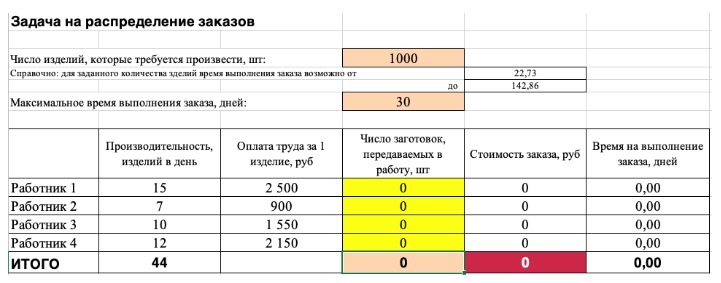
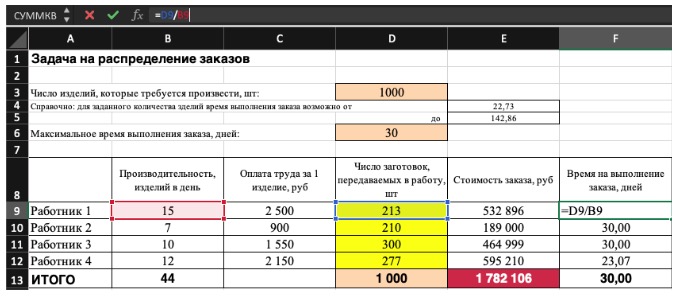
3) Выделите целевую ячейку, которая должна показать максимум, минимум или определенное значение при заданных условиях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

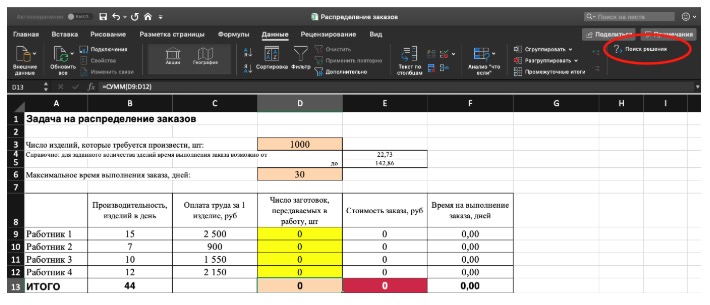
4) Заполните параметры «Поиска решений» и нажмите «Найти решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от каждого работника. Данная ячейка (Е13) — это целевая функция. D9:D12 — изменяемые ячейки. «Поиск решений» определяет их оптимальные значения, чтобы целевая функция достигла минимума при заданных ограничениях.

В нашем примере следующие ограничения:

• общее количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля либо равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше либо равно 30 ($F$9:$F$12 > окажут вам помощь. Это отличный шанс вместе экспертом проработать проблемные вопросы и составить карьерный план.

Поиск решения

1. Постройте и оформите следующую таблицу

                       

1. 1. Здесь в столбике График отмечены группы работников, во втором столбике       отмечены выходные дни у соответствующих групп (каждая группа должна иметь       два дня выходных, идущих друг за другом), в столбике Работники отмечено количество работников в каждой группе. а далее       цифра 1 означает, что данная группа в этот день работает, цифра 0 –       группа не работает. В ячейке C14 находится формула, вычисляющая общее       количество работников. В ячейке C15 – оплата труда одному человеку за неделю. В ячейке C15 – формула,       вычисляющая общую оплату работников за неделю.
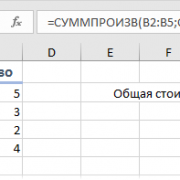
   2. Введите текст в клетки. Отформатируйте информацию       в клетках и выполните обрамление (и заливку) диапазонов ячеек так, как указано       в примечаниях (пункт меню Формат).       Ширину столбца можно изменить, установив курсор мыши на разделительную линию       в строке заголовков столбцов (курсор примет вид креста со стрелками) и,       при нажатой левой кнопке мыши, переместив ее в нужную сторону. В ячейки E14:K14 вставьте формулы для вычисления       суммарного количества сотрудников, работающих в соответствующий день       недели. Для вставки Вставка –       Функция.  Используйте функцию СУММПРОИЗВ. Скопируйте введенную       формулу в остальные ячейки диапазона, используя маркер копирования в правом       нижнем углу ячейки. Для правильного копирования формулы в данном случае       необходимо, чтобы в ссылке на диапазон C6:C12       использовались абсолютные адреса, т.е. ссылка должна иметь вид $C$6:$C$12.

1. Пусть требуется решить задачу о построении графика занятости персонала парка отдыха.

Для работников с пятидневной рабочей неделей и двумя выходными подряд требуется подобрать график работы, обеспечивающий требуемый уровень обслуживания при наименьших затратах на оплату труда (основные данные находятся в Таблице). В этом примере ставки ежедневной оплаты одинаковы, поэтому снижение числа ежедневно занятых сотрудников приводит к уменьшению затрат на персонал.

1. Пусть требуемый уровень обслуживания определяется заданным (для каждого дня недели) числом работников (22, 17, 13, 14, 15, 18, 24 соответственно в воскресенье, понедельник,…субботу). Дополните Таблицу. В ячейки E15:K15 введите значения 22, 17, 13, 14, 15, 18, 24. Для выделения ограничений выполните обрамление диапазона E14:K15 жирной красной линией.
2. Параметры задачи.

C16 — Расходы на оплату труда.

C6:C12 — Число работников в группе (изменяемые данные – неизвестные в задаче).

C6:C12>=0 (Число работников в группе не может быть отрицательным)

C6:C12=Целое  (Число работников должно быть целым.)

E14:K14>=E15:K15 (Число ежедневно занятых работников не должно быть меньше ежедневной потребности).

Выберите Сервис – Поиск решения. Установить целевую – С16. Изменяя ячейки – С6-С12. При помощи кнопки Добавить установите три ограничения – С6:С12>=0, С6:С12=Целое, E14:K14>=E15:K15

Поскольку ограничения и целевая функция линейно зависят от  неизвестных, в параметрах надстройки выберите линейную модель.

По окончании поиска решения сохраните результаты вычислений.

Чуть-чуть истории и теории.

Вы задумывались когда-нибудь — откуда и зачем в головах людей, живших в XVI…XVII веках, родились понятия дифференциалов, производных, интегралов? Объяснение, в общем-то, достаточно простое и понятное – эти ученые искали аналитические пути решения прикладных практических задач. И успешно находили!!!

Мне сегодня видится приблизительно такая «лестница» с качественными «ступенями инструментов» математики для решения практических и научных задач, которую изобрело человечество:

1. Арифметика — сложение, вычитание, умножение, деление.

2. Алгебра – применение элементарных функций (степенной, логарифмической, тригонометрической, …) и алгебраических уравнений функции одной переменной.

3. Гауссовские системы линейных уравнений.

4. Численные методы решения трансцендентных уравнений.

5. Численные методы решения систем трансцендентных уравнений функций нескольких переменных.

6. Дифференцирование и интегрирование функций одной переменной.

7. Дифференцирование и интегрирование функций нескольких переменных.

8. Системы дифференциальных и интегральных уравнений.

9. Масса разнообразных новых и старых специальных методик и подходов мне не известных и известных, но, безусловно, существующих и работающих.

Предлагаю остановиться и разобраться с достаточно высокой четвертой ступенью «лестницы».

Для численного решения нелинейных уравнений успешно применяются: метод половинного деления, метод простых итераций, метод хорд, метод касательных Ньютона, комбинированный метод секущих-хорд на основе итерационной формулы Ньютона. Для чего ученые-математики придумали множество различных методов решения трансцендентных уравнений? Они старались упростить и ускорить процесс расчетов. Надо помнить и понимать, что у них компьютеров не было, и расчеты выполнялись вручную.

Каждый из методов имеет свои достоинства и недостатки — они подробно описаны в литературе, и углубляться в них мы не будем. Скажу только, что из вышеперечисленных методов мне на практике довелось использовать все. При решении различных (в основном геометрических и теплотехнических) задач по разным причинам было удобно использовать то один, то другой подход. Метод Ньютона хорош своей быстрой сходимостью и простотой формулы. Комбинированный метод секущих-хорд на основе итерационной формулы Ньютона не требует нахождения производных, быстро «сходится», и главное – не требует анализа функции на сходимость. Метод половинного деления медленно сходится, но не требует никакого предварительного анализа функции.