Пример выполнения корреляционного анализа в excel

Краткий обзор ковариации, корреляции и причинно-следственной связи

В предыдущей статье мы обсудили ковариацию, корреляцию и причинно-следственную связь.

• Дисперсия количественно определяет мощность случайных отклонений в наборе данных.
• Ковариация количественно определяет взаимосвязь между отклонениями в двух отдельных наборах данных. Более конкретно, она фиксирует склонность значений в двух наборах данных к изменению вместе (то есть к совместному изменению) линейным образом.
• Ковариация измеряет корреляцию двух переменных.
• Корреляция не доказывает причинно-следственную связь – если две переменные коррелированы, мы не можем автоматически сделать вывод, что изменения в одной переменной вызывают изменения в другой переменной. Тем не менее, если мы подозреваем наличие причинно-следственной связи и можем продемонстрировать корреляцию, у нас есть веские основания для дальнейшего изучения возможности причинной связи путем сбора дополнительных данных или проведения новых экспериментов.

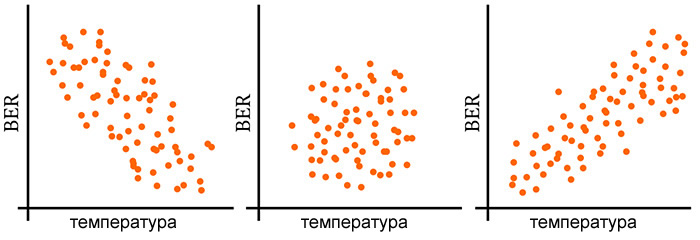Рисунок 1 – Примеры из предыдущей статьи отрицательной корреляции (слева), отсутствия корреляции (в центре) и положительной корреляции (справа). BER означает коэффициент битовых ошибок.

Графическое представление коэффициента Фехнера

Пример №1. При разработке глинистого раствора с пониженной водоотдачей в высокотемпературных условиях проводили параллельное испытание двух рецептур, одна из которых содержала 2% КМЦ и 1% Na2CO3, а другая 2% КМЦ, 1% Na2CO3 и 0,1% бихромата калия. В результате получена следующие значения Х (водоотдача через 30 с).

X1	9	9	11	9	8	11	10	8	10
X2	10	11	10	12	11	12	12	10	9

Пример №2.
Коэффициент корреляции знаков, или коэффициент Фехнера, основан на оценке степени согласованности направлений отклонений индивидуальных значений факторного и результативного признаков от соответствующих средних. Вычисляется он следующим образом:

,

где n_a — число совпадений знаков отклонений индивидуальных величин от средней; n_b — число несовпадений.

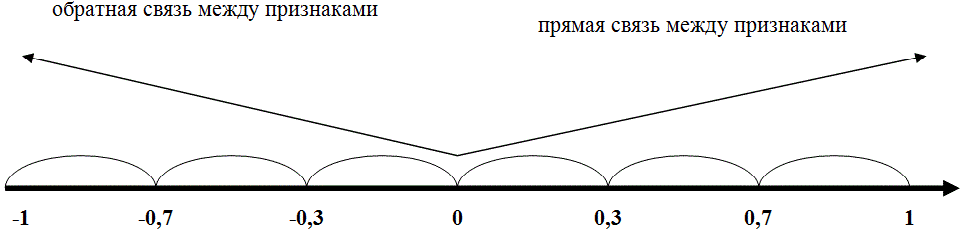
Коэффициент Фехнера может принимать значения от -1 до +1. Kф = 1 свидетельствует о возможном наличии прямой связи, Kф =-1 свидетельствует о возможном наличии обратной связи.

Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:

Xi	Yi	Знаки отклонений значений признака от средней	Совпадение (а) или несовпадение (в) знаков
Для Xi	Для Yi
8	40	—	—	А
9	50	—	+	В
10	48	—	+	В
10	52	—	+	В
11	41	+	—	В
13	30	+	—	В
15	35	+	—	В

Для примера: .

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Пример №2
Рассмотрим на примере расчет коэффициента Фехнера по данным, приведенным в таблице:
Средние значения:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
12	220	+	—	B
9	1070	—	+	B
8	1000	—	+	B
14	606	+	—	B
15	780	+	+	A
10	790	—	+	B
10	900	—	+	B
15	544	+	—	B
93	5910

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Интервальная оценка для коэффициента корреляции знаков

Пример №3.
Рассмотрим на примере расчет коэффициента корреляции знаков по данным, приведенным в таблице:

Xi	Yi	Знаки отклонений от средней X	Знаки отклонений от средней Y	Совпадение (а) или несовпадение (b) знаков
96	220	+	—	B
52	1070	—	+	B
60	1000	—	+	B
89	606	+	—	B
82	780	+	+	A
77	790	—	+	B
70	900	—	+	B
92	544	+	—	B
618	5910

Значение коэффициента свидетельствует о том, что можно предполагать наличие обратной связи.

Оценка коэффициента корреляции знаков. Значимость коэффициента корреляции знаков.
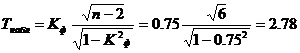По таблице Стьюдента находим t_табл:
t_табл (n-m-1;a) = (6;0.05) = 1.943
Поскольку Tнабл > tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции знаков. Другими словами, коэффициент корреляции знаков статистически — значим.

Доверительный интервал для коэффициента корреляции знаков.
Доверительный интервал для коэффициента корреляции знаков.
r(-1;-0.4495)

Блог о программе Microsoft Excel: приемы, хитрости, секреты, трюки

В сегодняшней статье речь пойдет о том, как переменные могут быть связаны друг с другом. С помощью корреляции мы сможем определить, существует ли связь между первой и второй переменной. Надеюсь, это занятие покажется вам не менее увлекательным, чем предыдущие!

Корреляция измеряет мощность и направление связи между x и y. На рисунке представлены различные типы корреляции в виде графиков рассеяния упорядоченных пар (x, y). По традиции переменная х размещается на горизонтальной оси, а y — на вертикальной.

График А являет собой пример положительной линейной корреляции: при увеличении х также увеличивается у, причем линейно. График В показывает нам пример отрицательной линейной корреляции, на котором при увеличении х у линейно уменьшается. На графике С мы видим отсутствие корреляции между х и у. Эти переменные никоим образом не влияют друг на друга.

Наконец, график D — это пример нелинейных отношений между переменными. По мере увеличения х у сначала уменьшается, потом меняет направление и увеличивается.

Оставшаяся часть статьи посвящена линейным взаимосвязям между зависимой и независимой переменными.

Коэффициент корреляции

Коэффициент корреляции, r, предоставляет нам как силу, так и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между — 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной (график A на рисунке), а когда значение r отрицательно, связь также отрицательна (график В). Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует график С).

Сила связи между х и у определяется близостью коэффициента корреляции к — 1.0 или +- 1.0. Изучите следующий рисунок.

График A показывает идеальную положительную корреляцию между х и у при r = + 1.0. График В — идеальная отрицательная корреляция между х и у при r = — 1.0. Графики С и D — примеры более слабых связей между зависимой и независимой переменными.

Коэффициент корреляции, r, определяет, как силу, так и направление связи между зависимой и независимой переменными. Значения r находятся в диапазоне от — 1.0 (сильная отрицательная связь) до + 1.0 (сильная положительная связь). При r= 0 между переменными х и у нет никакой связи.

Мы можем вычислить фактический коэффициент корреляции с помощью следующего уравнения:

Ну и ну! Я знаю, что выглядит это уравнение как страшное нагромождение непонятных символов, но прежде чем ударяться в панику, давайте применим к нему пример с экзаменационной оценкой. Допустим, я хочу определить, существует ли связь между количеством часов, посвященных студентом изучению статистики, и финальной экзаменационной оценкой. Таблица, представленная ниже, поможет нам разбить это уравнение на несколько несложных вычислений и сделать их более управляемыми.

Как видите, между числом часов, посвященных изучению предмета, и экзаменационной оценкой существует весьма сильная положительная корреляция. Преподаватели будут весьма рады узнать об этом.

Какова выгода устанавливать связь между подобными переменными? Отличный вопрос. Если обнаруживается, что связь существует, мы можем предугадать экзаменационные результаты на основе определенного количества часов, посвященных изучению предмета. Проще говоря, чем сильнее связь, тем точнее будет наше предсказание.

Использование Excel для вычисления коэффициентов корреляции

Я уверен, что, взглянув на эти ужасные вычисления коэффициентов корреляции, вы испытаете истинную радость, узнав, что программа Excel может выполнить за вас всю эту работу с помощью функции КОРРЕЛ со следующими характеристиками:

КОРРЕЛ (массив 1; массив 2),

массив 1 = диапазон данных для первой переменной,

массив 2 = диапазон данных для второй переменной.

Например, на рисунке показана функция КОРРЕЛ, используемая при вычислении коэффициента корреляции для примера с экзаменационной оценкой.

1) Эмпирический коэффициент детерминации:

 – есть отношение межгрупповой дисперсии к общей дисперсии.

Общая дисперсия  учитывает ВСЕ причины, которые влияют на вариацию признака-результата (прибыли). Межгрупповая дисперсия  учитывает влияние фактора, положенного в основу группировки (выпуска продукции).

Эмпирический коэффициент детерминации характеризует ДОЛЮ влияния группировочного фактора (выпуска продукции). Данный коэффициент изменяется в пределах , и чем он ближе к единице, тем сильнее влияние группировочного фактора на признак-результат (прибыль).

Дело за малым – вычислить  и .

В «шапке» и в левом столбце комбинационной таблицы (см. выше) у нас находятся два интервальных вариационных ряда и сначала нужно перейти к дискретным рядам, выбрав в качестве вариант  и  середины соответствующих интервалов: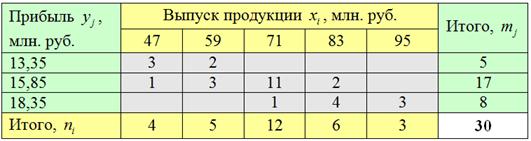

На всякий случай примеры расчёта: .

Вычислим общую среднюю признака-результата: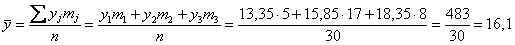 млн. руб.

и общую дисперсию: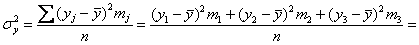

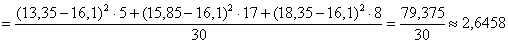
Разбираемся с межгрупповой дисперсией. Для её нахождения вычислим групповые или, как их называют, условные средние. При условии  средняя прибыль составит: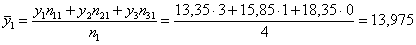 млн. руб.
и давайте ещё в качестве закрепляющего примера приведу расчёт для :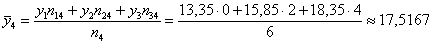 млн. руб.

Промежуточные вычисления удобно заносить рядышком, наращивая комбинационную таблицу: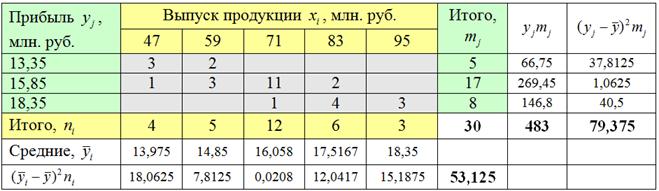

Полагаю, после моих видео вам не составит труда автоматизировать эти вычисления в Экселе. Вычислим межгрупповую дисперсию: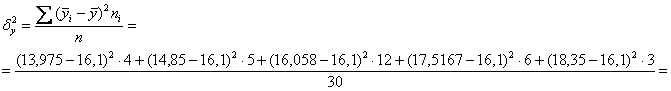

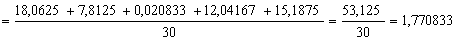
В качестве факультативного задания предлагаю самостоятельно вычислить групповые дисперсии ( по каждой из пяти групп), внутригрупповую дисперсию и проверить правило сложения дисперсий . Я выполнил это в обязательном порядке, дабы избежать ошибок.

Вычислим эмпирический коэффициент детерминации: – таким образом, 66,93% вариации прибыли обусловлено изменением  выпуска продукции. Остальные 33,07% вариации обусловлены другими факторами.

Исходя из правило сложения дисперсий , легко понять, что за остальную вариацию отвечает внутригрупповая дисперсия , графически она характеризует меру разброса частот в серых столбцах (см. таблицу выше).

Теперь повторим суть коэффициента детерминации. Чем ближе  к единице, тем больше межгрупповая дисперсия  и меньше . Высокое значение  говорит о том, что групповые средние  знАчимо отличаются от общей средней , то есть изменение значений «икс» приводит к существенному изменению значений «игрек». Иными словами, признак-фактор действительно оказывает сильное влияние. При этом внутригрупповая  дисперсия  будет малА и частоты в серой области примут выраженный диагональный вид. В предельном случае   (и нулевом значении ) речь идёт о строгой функциональной зависимости.

Обратно, малые значения  обусловлены тем, что межгрупповая дисперсия  близкА к нулю – по той причине, что групповые средние  близкИ к общей средней . Это означает, что на изменение значений «икс» – «игреки» «откликаются» слабо. При этом внутригрупповая дисперсия  будет большой – это значит, что дисперсия в группах существенна и частоты в серых столбцах более разбросаны – фактически они заполнят всю серую область и, естественно, утратят диагональный вид.

Кто всё понял, тот монстр 🙂

Следующий показатель:

Примеры

Допустим, в каком-то эксперименте в равные промежутки времени измеряют две величины, X и Y. Если их значения меняются, как на этом графике, то это полностью коррелированные величины с
коэффициентом корреляции, равным +1.

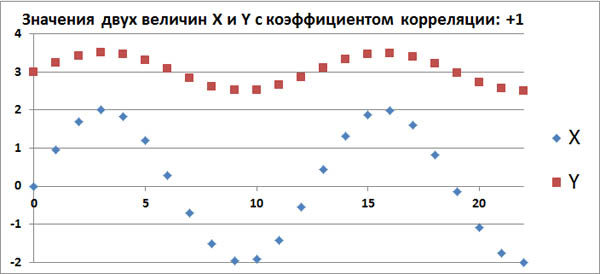
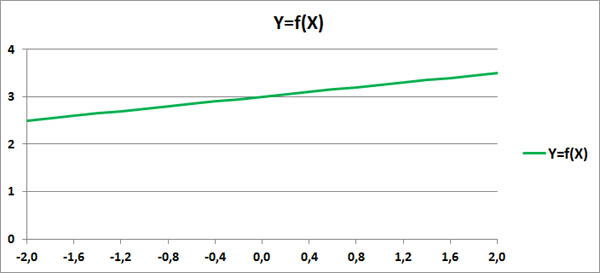
Этот факт говорит о том, что между величинами X и Y имеется строгая функциональная зависимость: Y=f(X).

Допустим, в каком-то эксперименте в равные промежутки времени измеряют две величины, X и Y. Если их значения меняются, как на следующем графике, то это полностью антикоррелированные величины
с коэффициентом корреляции, равным -1.

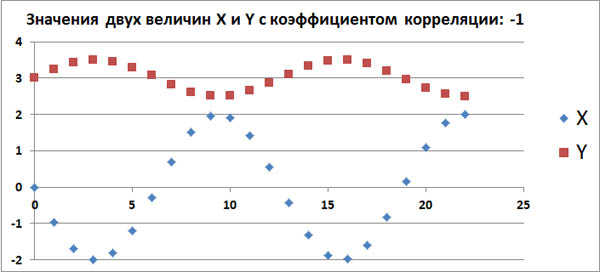
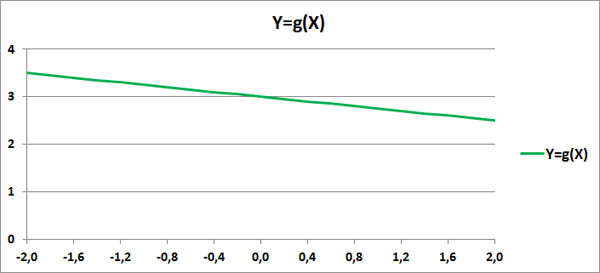
Этот факт также говорит о том, что между величинами X и Y имеется какая-то строгая функциональная зависимость: Y=g(X).

Теперь рассмотрим реальные цены. Для примера рассмотрим коэффициенты корреляции между ценами валютной пары EURUSD и ценами валютных пар GBPUSD, USDCHF и USDJPY. Для расчета возьмем дневные графики за
первую половину 2017 года.

EURUSD

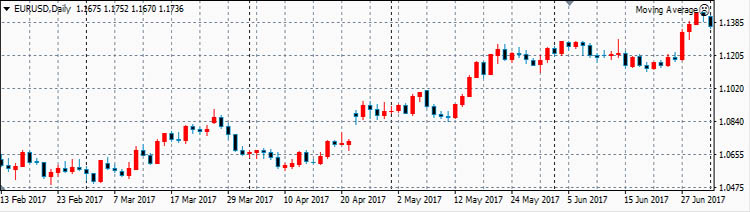
GBPUSD

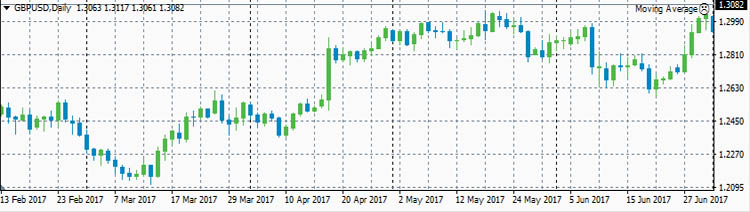
USDCHF

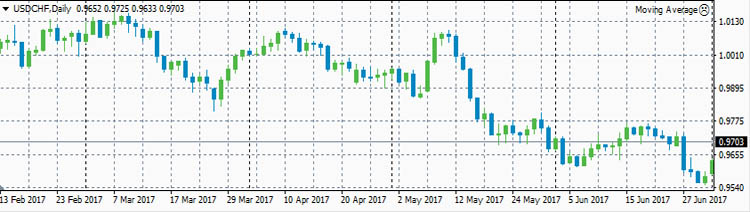
USDJPY

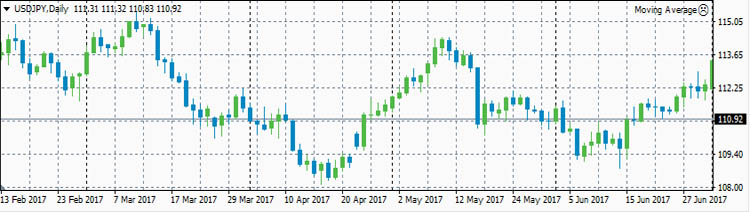
Расчеты, сделанные по ценам закрытия тайм-фреймов дают следующие коэффициенты корреляции за полгода:

• ρ(eurusd,gbpusd)=0.8030
• ρ(eurusd,usdchf)=-0.9598
• ρ(eurusd,usdjpy)=-0.4802

Эти коэффициенты корреляции достаточно ожидаемые.

Достаточно сильная корреляция между EURUSD и GBPUSD объясняется достаточно сильными связями экономики ЕвроЗоны и экономики Британии. Очень сильная антикорреляция между EURUSD и USDCHF объясняется еще
более сильной связью между экономиками ЕвроЗоны и Швейцарии. А знак минус получился потому что в валютной паре USDCHF швейцарский франк стоит в знаменателе, в то время как в валютной паре EURUSD евро
стоит в числителе.

Интересно посмотреть не только коэффициенты корреляции разных валютных пар, но и то, как эти коэффициенты изменяются со временем. Для этого возьмем внутри полугодового периода трехмесячный период и
посмотрим, как меняется коэффициент корреляции, если сдвигать этот трехмесячный период от начала полугодового периода до его конца. Всего за полгода будет 65 таких сдвижек.

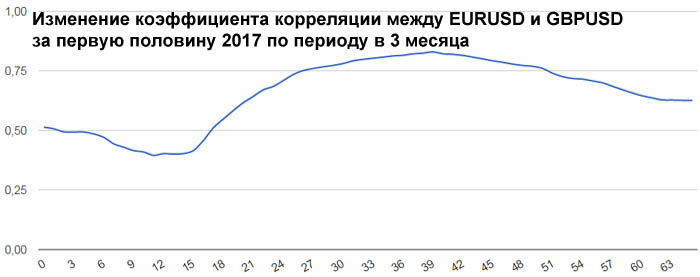
В начале 2017 года корреляция между EURUSD и GBPUSD была небольшой и она даже немного уменьшалась. Но в середине полугодия корреляция между евро и фунтом усилилась. Таким образом, в определенное время
фунт может не слишком хорошо коррелировать с евро.

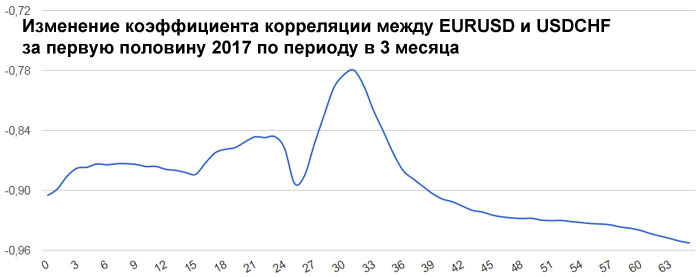
А вот в первую половину 2017 года швейцарский франк оказался привязанным к евро очень сильно. Коэффициент корреляции менялся в пределах от -0.96 до -0.78. Это и понятно, ведь Швейцария со всех сторон
окружена ЕвроЗоной. Поэтому её экономика должна быть сильно связана с экономикой ЕвроЗоны. Гораздо сильнее, чем британская экономика с экономикой ЕвроЗоны.

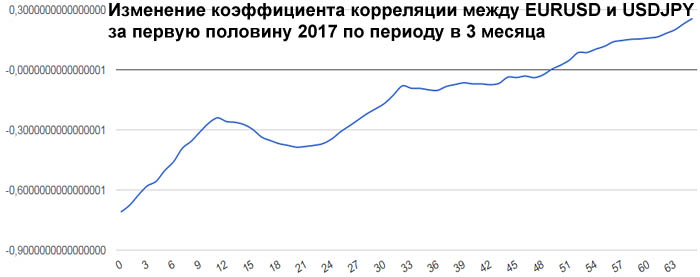
А вот что касается евро и йены, то тут ситуация самая интересная. В начале первого полугодия 2017 года была антикорреляция выше средней, примерно -0.71. Потом эта антикорреляция исчезла до нуля. Но на
этом изменения коэффициента корреляции не остановились. Коэффициент корреляции вырос до +0.2564. Так как евро в валютной паре EURUSD находится в числителе, а йена в валютной паре USDJPY находится в
знаменателе, то получается, что в начале года евро и йена сильно коррелировали, а к середине года стали слегка антикоррелировать.

9.1.2. Проверка статистических гипотез о связи переменных

Выборочный коэффициент корреляции оценивает подразумеваемую исследователем реальную связь между переменными. Как и в случае оценки среднего значения, нас интересуют два вопроса: (1) Насколько сильна связь между переменными; (2) Насколько надежна наша оценка. Сила связи между переменными по всей генеральной совокупности существует объективно. Если ее измерять корреляцией, то она будет выражаться числом от −1 до 1. Выборочная корреляция этих переменных будет колебаться вокруг истинного показателя силы связи. Трудность состоит в том, что, получив выборочную корреляцию, мы не можем знать, ни насколько она отклоняется от истинного значения, ни даже в какую сторону. В случае корреляции оценка обычно выражается в терминах значимости.

Проделаем небольшое упражнение.

Упражнение 9.1.2(1). Возьмите две симметричные монеты достоинством в один рубль и один евро. Проведите серию четырех подбрасываний пары монет и запишите результаты в виде ​\( (x_1, y_1),\dots,(x_4, y_4) \)​ , полагая

​\( x_i=0 \)​, если рубль выпал цифрой;

​\( x_i=1 \), если рубль выпал гербом;

​\( y_i=0 \), если евро выпал цифрой;

​\( y_i=1 \), если евро выпал гербом.

Подсчитайте коэффициент корреляции Пирсона. Истинная корреляция между результатами двух монет равна, разумеется, нулю. Повторите процедуру несколько раз и убедитесь, что нулевое значение выборочного коэффициента корреляции выпадает примерно один раз из трех. При многократном повторении опыта можно убедиться, что его результат имеет некоторое распределение, симметричное относительно нуля. Это распределение зависит от объема выборки n: чем больше n, тем меньше дисперсия распределения, тем ближе к нулю ее вероятные значения.

В таблице 9.1.2(2) приведены двухсторонние квантили распределения выборочного коэффициента корреляции по Пирсону для ​\( n=10 \)​. Они рассчитаны для выборок, полученных испытаниями двух нормально распределенных случайных величин, теоретическая корреляция между которыми равна нулю. Дихотомический результат подбрасывания монеты не распределен нормально, однако некоторое представление о возможных результатах наших испытаний табличный квантиль все же дает.

Таблица 9.1.2(2) Двусторонние квантили распределения коэффициента Пирсона для n = 10

​\( \alpha \)​	0.05	0.025	0.01	0.005
​\( r_\alpha(10) \)​	0.497	0.576	0.658	0.709

Обычно при исследовании связи переменных статистической гипотезой ​\( H_0 \)​ будет гипотеза об отсутствии связи, т.е. о независимости переменных. Альтернативная гипотеза \( H_1 \)​ (т.е. гипотеза, к которой мы склоняемся, получив большие по модулю значения выборочной корреляции) будет утверждать только наличие связи . Можно оценить значимость относительно данного результата (полученной парной выборки) гипотез о других значениях теоретической корреляции, но это требует некоторых дополнительных усилий (см. подпараграф ). Если истинна гипотеза \( H_0 \)​, то выборочный коэффициент корреляции будет принимать значения, более или менее близкие к нулю. Если выборочная корреляция принимает достаточно большое по модулю значение, которому соответствует значимость, измеряемая маленьким числом, то мы склоняемся к гипотезе \( H_1 \)​ о наличии связи, но без указания точного значения теоретической корреляции.

Можно заметить, что если верна гипотеза  об отсутствии зависимости между случайными величинами, то выборочный коэффициент при \( n=10 \) может принимать тем не менее довольно большие значения, так что уровень значимости 0.05 для принятия гипотезы о зависимости случайных величин требует, чтобы выборочный коэффициент корреляции достигал почти 0.5 (см. ). В связи с этим надо иметь в виду, что даже выборочная корреляция, например 0.6, вполне может согласовываться с истинной корреляцией, равной 0.2 .

Распространенные ошибки с корреляцией

Самая распространенная ошибка – это предположение, что корреляция, приближающаяся к +/- 1, является статистически значимой. Показание, приближающееся к +/- 1, определенно увеличивает шансы на фактическую статистическую значимость, но без дальнейшего тестирования это невозможно узнать.

Статистическая проверка корреляции может усложняться по ряду причин; это совсем не просто

Важное предположение о корреляции состоит в том, что переменные независимы и что связь между ними линейна. Теоретически вы должны проверить эти утверждения, чтобы определить, подходит ли расчет корреляции

Краткий обзор

Помните, что корреляция между двумя переменными НЕ означает, что A вызвало B или наоборот.

Вторая наиболее частая ошибка – это забвение нормализовать данные в единый блок. Если вычисляется корреляция для двух бета-версий, то единицы уже нормализованы: сама бета является единицей

Однако, если вы хотите соотнести акции, очень важно нормализовать их в процентах доходности, а не в изменении цены акций. Это случается слишком часто даже среди профессионалов в области инвестиций

Что касается корреляции цен на акции, вы, по сути, задаете два вопроса: какова доходность за определенное количество периодов и как эта доходность соотносится с доходностью другой ценной бумаги за тот же период?

По этой же причине трудно установить корреляцию цен на акции: две ценные бумаги могут иметь высокую корреляцию, если доходность представляет собой ежедневные процентные изменения за последние 52 недели, но низкая корреляция, если доходность представляет собой ежемесячные изменения за последние 52 недели. Какой из них лучше”? На самом деле нет идеального ответа, и это зависит от цели теста.

Поиск корреляции в Excel

Существует несколько методов расчета корреляции в Excel. Самый простой – получить два набора данных бок о бок и использовать встроенную формулу корреляции:

Это удобный способ вычислить корреляцию между двумя наборами данных. Но что, если вы хотите создать корреляционную матрицу для ряда наборов данных? Для этого вам необходимо использовать плагин анализа данных Excel. Плагин можно найти на вкладке «Данные» в разделе «Анализ».

Выберите таблицу доходов. В этом случае наши столбцы имеют заголовки, поэтому мы хотим установить флажок «Ярлыки в первой строке», чтобы Excel обрабатывал их как заголовки. Затем вы можете выбрать вывод на том же листе или на новом листе.

Как только вы нажмете Enter, данные будут созданы автоматически. Вы можете добавить текст и условное форматирование, чтобы очистить результат.

Ссылки

Hardoon D., Szedmak S., Shawe-Taylor J. Canonical Correlation Analysis: An Overview with Application to Learning Methods // Neural Computation. — 2004. — Т. 16, вып. 12. — P. 2639–2664. — DOI:10.1162/0899766042321814. — PMID 15516276.
A note on the ordinal canonical-correlation analysis of two sets of ranking scores (Приведена программа на языке FORTRAN)- Journal of Quantitative Economics 7(2), 2009, pp. 173–199
Representation-Constrained Canonical Correlation Analysis: A Hybridization of Canonical Correlation and Principal Component Analyses (Приведена программа на языке FORTRAN)- Journal of Applied Economic Sciences 4(1), 2009, стр. 115–124

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии. Проверить статью на грамматические и орфографические ошибки.

Значения коэффициента корреляции

Охарактеризовать силу корреляционной связи можно прибегнув к шкале Челдока, в которой определенному числовому значению соответствует качественная характеристика.

• 0-0,3 – корреляционная связь очень слабая;
• 0,3-0,5 – слабая;
• 0,5-0,7 – средней силы;
• 0,7-0,9 – высокая;
• 0,9-1 – очень высокая сила корреляции.

Шкала может использоваться и для отрицательной корреляции. В этом случае качественные характеристики заменяются на противоположные.

Можно воспользоваться упрощенной шкалой Челдока, в которой выделяется всего 3 градации силы корреляционной связи:

• очень сильная – показатели ±0,7 — ±1;
• средняя – показатели ±0,3 — ±0,699;
• очень слабая – показатели 0 — ±0,299.

Данный статистический показатель позволяет не только проверить предположение о существовании линейной взаимосвязи между признаками, но и установить ее силу.

История разработки критерия корреляции

Критерий корреляции Пирсона был разработан командой британских ученых во главе с Карлом Пирсоном (1857-1936) в 90-х годах 19-го века, для упрощения анализа ковариации двух случайных величин. Помимо Карла Пирсона над критерием корреляции Пирсона работали также Фрэнсис Эджуорт и Рафаэль Уэлдон.

Для чего используется критерий корреляции Пирсона?

Критерий корреляции Пирсона позволяет определить, какова теснота (или сила) корреляционной связи между двумя показателями, измеренными в количественной шкале. При помощи дополнительных расчетов можно также определить, насколько статистически значима выявленная связь.

Например, при помощи критерия корреляции Пирсона можно ответить на вопрос о наличии связи между температурой тела и содержанием лейкоцитов в крови при острых респираторных инфекциях, между ростом и весом пациента, между содержанием в питьевой воде фтора и заболеваемостью населения кариесом.

Условия и ограничения применения критерия хи-квадрат Пирсона

1. Сопоставляемые показатели должны быть измерены в количественной шкале (например, частота сердечных сокращений, температура тела, содержание лейкоцитов в 1 мл крови, систолическое артериальное давление).
2. Посредством критерия корреляции Пирсона можно определить лишь наличие и силу линейной взаимосвязи между величинами. Прочие характеристики связи, в том числе направление (прямая или обратная), характер изменений (прямолинейный или криволинейный), а также наличие зависимости одной переменной от другой – определяются при помощи регрессионного анализа.
3. Количество сопоставляемых величин должно быть равно двум. В случае анализ взаимосвязи трех и более параметров следует воспользоваться методом факторного анализа.
4. Критерий корреляции Пирсона является параметрическим, в связи с чем условием его применения служит нормальное распределение каждой из сопоставляемых переменных. В случае необходимости корреляционного анализа показателей, распределение которых отличается от нормального, в том числе измеренных в порядковой шкале, следует использовать коэффициент ранговой корреляции Спирмена.
5. Следует четко различать понятия зависимости и корреляции. Зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот.

Например, рост ребенка зависит от его возраста, то есть чем старше ребенок, тем он выше. Если мы возьмем двух детей разного возраста, то с высокой долей вероятности рост старшего ребенка будет больше, чем у младшего. Данное явление и называется зависимостью, подразумевающей причинно-следственную связь между показателями. Разумеется, между ними имеется и корреляционная связь, означающая, что изменения одного показателя сопровождаются изменениями другого показателя.

В другой ситуации рассмотрим связь роста ребенка и частоты сердечных сокращений (ЧСС). Как известно, обе эти величины напрямую зависят от возраста, поэтому в большинстве случаев дети большего роста (а значит и более старшего возраста) будут иметь меньшие значения ЧСС. То есть, корреляционная связь будет наблюдаться и может иметь достаточно высокую тесноту. Однако, если мы возьмем детей одного возраста, но разного роста, то, скорее всего, ЧСС у них будет различаться несущественно, в связи с чем можно сделать вывод о независимости ЧСС от роста.

Приведенный пример показывает, как важно различать фундаментальные в статистике понятия связи и зависимости показателей для построения верных выводов

Коэффициент корреляции в Excel и формула расчёта

Вероятно, вас интересует, как самостоятельно рассчитать корреляцию двух инвестиционных активов. До изобретения компьютеров приходилось делать это вручную, для чего использовалась вот такая формула коэффициента корреляции:

• Rxy — коэффициент корреляции;
• COVxy — ковариация переменных X и Y;
• σX, σY — стандартное отклонение переменных X и Y
• X и Y с чертой — среднее значение Х и Y

Кстати, студентам на экзамене до сих пор компьютеров не выдают, хоть калькулятор можно и на том спасибо. Как вы понимаете, занятие все равно трудоёмкое 🙂

Профессиональному инвестору может понадобиться рассчитать сотни корреляций, так что вариант по формуле не подходит. Естественно, эта задача уже давно автоматизирована, и, как по мне, проще всего рассчитать коэффициент корреляции в Excel.

Чтобы далеко за примером не ходить, давайте рассчитаем корреляцию двух популярных ПАММ-счетов и Hohla EUR. Они находятся на площадке компании Alpari, а значит мы можем скачать историю доходности прямо с сайта:

Далее нам надо скопировать историю доходности в один файл, для удобства. Для точного расчета корреляции в Excel нам в принципе хватит и двух лет истории, располагаем данные так:

Теперь, как я уже писал выше, для ПАММ-счетов (и для многих других инвестиционных инструментов) надо рассчитать дневные доходности:

А дальше все просто — используется встроенная формула коэффицента корреляции в Excel =КОРРЕЛ():

Получили значение 0.12, а значит стратегии ПАММ-счетов практически не имеют ничего общего. Это хорошо для диверсификации, так что можно добавлять обоих в инвестиционный портфель.

При желании, можно сделать табличку на весь ваш портфель. Тогда если у вас появится новый вариант для инвестирования, вы сможете сразу сравнить его с каждым активом и увидеть, есть ли нежелательные корреляции.

До встречи и успешных вам инвестиций!

Формула корреляции

рзнак равно∑(Икс-Икс‾)(Y-Y‾)∑(Икс-Икс‾)2(Y-Y‾)2жчере:рзнак равнотче соттелтяонгрöеффягряент Икс‾знак равнотчеобергеоеоБсекегобтяопыоеобгябле      ИксY‾знак равнотчеобергеоеоБсекегобтяопыоеобгябле      Y\ begin {align} & r = \ frac {\ sum (X – \ overline {X}) (Y – \ overline {Y})} {\ sqrt {\ sum (X – \ overline {X}) ^ 2} \ sqrt {(Y – \ overline {Y}) ^ 2}} \\ & \ textbf {где:} \\ & r = \ text {коэффициент корреляции} \\ & \ overline {X} = \ text {среднее значение наблюдения переменной} X \\ & \ overline {Y} = \ text {среднее значение наблюдений переменной} Y \\ \ end {выровнено}Взаимодействие с другими людьмирзнак равно∑(X-Икс

158.7,102.5,238c34.3,79.3,51.8,119.3,52.5,120c340,-704.7,510.7,-1060.3,512,-1067
c4.7,-7.3,11,-11,19,-11H40000v40H1012.3s-271.3,567,-271.3,567c-38.7,80.7,-84,
175,-136,283c-52,108,-89.167,185.3,-111.5,232c-22.3,46.7,-33.8,70.3,-34.5,71
c-4.7,4.7,-12.3,7,-23,7s-12,-1,-12,-1s-109,-253,-109,-253c-72.7,-168,-109.3,
-252,-110,-252c-10.7,8,-22,16.7,-34,26c-22,17.3,-33.3,26,-34,26s-26,-26,-26,-26
s76,-59,76,-59s76,-60,76,-60z M1001 80H40000v40H1012z”>
158.7,102.5,238c34.3,79.3,51.8,119.3,52.5,120c340,-704.7,510.7,-1060.3,512,-1067
c4.7,-7.3,11,-11,19,-11H40000v40H1012.3s-271.3,567,-271.3,567c-38.7,80.7,-84,
175,-136,283c-52,108,-89.167,185.3,-111.5,232c-22.3,46.7,-33.8,70.3,-34.5,71
c-4.7,4.7,-12.3,7,-23,7s-12,-1,-12,-1s-109,-253,-109,-253c-72.7,-168,-109.3,
-252,-110,-252c-10.7,8,-22,16.7,-34,26c-22,17.3,-33.3,26,-34,26s-26,-26,-26,-26
s76,-59,76,-59s76,-60,76,-60z M1001 80H40000v40H1012z”>

Анализ полученных результатов

После корректного заполнения всех параметров и нажатия кнопки OK отобразятся результаты анализа (в зависимости от выбранного способа). В нашем случае – на отдельном листе.

Ключевым показателем здесь является R-квадрат (коэффициент детерминации), значение которого характеризует качество модели. Приемлемым считается значение не менее 0,5 (или 50%).

Также следует обратить внимание на ячейку, расположенную на пересечении строки “Y-пересечение” и столбца “Коэффициенты”. Здесь показывается, каким будет значение Y (количество осадков), если все остальные факторы будут равны нулю

Ячейка на пересечении строки “Переменная X 1” и столбца “Коэффициенты” содержит значение, характеризующее степень зависимости Y от X. Коэф. 0,89 в нашем случае говорит о достаточно сильной связи между переменными.

Корреляция и диверсификация

Как знания о корреляции активов могут помочь лучше вкладывать деньги? Думаю, вы все хорошо знакомы с золотым правилом инвестора — не клади все яйца в одну корзину. Речь, естественно, идёт о диверсификации инвестиционных активов в портфеле. Корреляция и диверсификация неразрывно связаны, что понятно даже из названия — английское diversify означает «разнообразить», а как коэффициент корреляции как раз показывает схожесть или различие двух явлений.

Другими словами, инвестировать в финансовые инструменты с высокой корреляцией не очень хорошо. Почему? Все просто — похожие активы плохо диверсифицируются. Вот пример портфеля двух активов с корреляцией +1:

Как видите, график портфеля во всех деталях повторяет графики каждого из активов — рост и падение обоих активов синхронны. Диверсификация в теории должна снижать инвестиционные риски за счёт того, что убытки одного актива перекрываются за счёт прибыли другого, но здесь этого не происходит совершенно. Все показатели просто усредняются:

Портфель даёт небольшой выигрыш в снижении рисков — но только по сравнению с более доходным Активом 1. А так, никаких преимуществ по сути нет, нам лучше просто вложить все деньги в Актив 1 и не париться.

А вот пример портфеля двух активов с корреляцией близкой к 0:

Где-то графики следуют друг за другом, где-то в противоположных направлениях, какой-либо однозначной связи не наблюдается. И вот здесь диверсификация уже работает:

Мы видим заметное снижение СКО, а значит портфель будет менее волатильным и более стабильно расти. Также видим небольшое снижение максимальной просадки, особенно если сравнивать с Активом 1. Инвестиционные инструменты без корреляции достаточно часто встречаются и из них имеет смысл составлять портфель.

Впрочем, это не предел. Наиболее эффективный инвестиционный портфель можно получить, используя активы с корреляцией -1:

Уже знакомое вам «зеркало» позволяет довести показатели риска портфеля до минимальных:

Несмотря на то, что каждый из активов обладает определенным риском, портфель получился фактически безрисковым. Какая-то магия, не правда ли? Очень жаль, но на практике такого не бывает, иначе инвестирование было бы слишком лёгким занятием.