Калькулятор комплексных чисел. вычисление выражений с комплексными числами

Мир математики

Достойный внимания сайт, предоставляющий после полученного ответа подробные пояснения. Работать с ним также очень легко:

вводите условия в соответствующие поля;

• выбираете нужное действие;
• после нажатия на выбранную операцию будет начато вычисление и выдан результат.

Здесь вы найдете при необходимости подробную инструкцию для работы, так что точно не запутаетесь. Доступны разные варианты вычислительных сервисов, к примеру, матричный, инженерный и прочие.

Полезный контент:

• Формат heic, чем открыть, что это такое?
• Перевод с английского на русский с транскрипцией — лучшие онлайн сервисы
• Видеодрайвер перестал отвечать и был восстановлен — что за ошибка?
• Запись видео с экрана компьютера — какие программы в этом помогут?
• Караоке онлайн петь бесплатно с баллами — какие сервисы в этом помогут

Операции с комплексными числами

Так же как и для вещественных чисел, для комплексных чисел определены операции сложения, вычитания, умножения и деления. Однако многие свойства комплексных чисел отличаются от свойств вещественных чисел. Например, нельзя указать, какое из двух комплексных чисел больше или меньше.

Сложение и вычитание комплексных чисел

Комплексные числа могут складываться и вычитаться как обычные.

Рассмотрим точку, обозначающую число 1+2i. Прибавим к нему число 3+1i. Можно сложить столбиком и получить 4+3i. Геометрически это обычное сложение векторов.

Разность комплексных чисел, записанных в алгебраической форме, представляет собой комплексное число, действительная часть которого и коэффициент при мнимой части равны соответственно разности действительных частей и разности коэффициентов при мнимой части уменьшаемого и вычитаемого.

В общем виде вычитание комплексных чисел z1 = a+bi и z2 = c+di можно записать так: z1-z2 = (a+bi)-(c+di) = (a-c)+(b-d)i.

Несколько примеров вычитания:

• (5+9i)-(3+24i) = (5-3)+(9-24)i = 2-15i.
• (-4+16i)-(11-8i) = (-4-11)+(16+8)i = -15+24i.

Умножение и деление комплексных чисел

Комплексные числа перемежаются точно также, как и действительные числа. Рассмотрим несколько примеров.

2×(1+1i) = 2+2i. Геометрически умножение на два выглядит как растягивание прямой с точкой на плоскости в два раза.

Умножать на i также не сложно. Известно, что i отвечает четверти оборота. Например, чтобы умножить 3+1i на i, достаточно повернуть точку на четверть оборота. Получаем -1+3i.

Умножим два комплексных числа 2+1,5i и -1+2,4i:

Сначала нужно умножить (-1+2,4 i) на два, затем на 1,5i. Далее складываются результаты. (2+1,5i)×(-1+2,4i) = 2(-1+2,4i)+1,5i(-1+2,4i) = -2+4,8i-1,5i+3,6×i×i. i в квадрате равно минус 1. Соответственно -2+4,8i-1,5i+3,6×i×i = -2+4,8i-1,5i-3,6 = -5,6+3,3i.

Частное комплексных чисел z1 = x1+y1i и z2 = x2+y2i в алгебраической форме находится путем домножения числителя и знаменателя на сопряженное число к знаменателю:

z1÷z2 = (x1+y1i)÷(x2+y2i) = ((x1+y1i)×(x2-y2i))÷((x2+y2i)×(x2-y2i)) = ((x1×x2+y1×y2)÷(x2²+y2²)) + (i×(x2×y1-x1×y2)÷(x2²+y2²)).

Рассмотрим пример деления -1+3i на 1+2i. Используя формулу для нахождения частного, получаем:

z1÷z2 = (-1+3i)÷(1+2i) = ((-1+3i)×(1-2i))÷((1+2i)×(1-2i)) = ((-1×1+3×2)÷(1²+2²))+(i×(3×1+(-1)×(-2))÷(1²+2²)) = 5÷5+i×5÷5 = 1+i.

Основные действия с комплексными числами

Основными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел. Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

• сложение: (a + bi) + (c + di) = (a + c) + (b + d)i
• вычитание: (a + bi) — (c + di) = (a — c) + (b — d)i
• умножение: (a + bi) · (c + di) = ac + bci + adi + bdi2 = (ac — bd) + (bc + ad)i
• деление:
  a + bi
  c + di
  =
  (a + bi)(c — di)
  c2 + d2
  =
  (ac + bd)
  c2 + d2
  +
  (bc — ad)
  c2 + d2
  i

Примеры

Найти сумму чисел и :
Найдём отдельно суммы действительных частей и сумму мнимых частей: re = 5 + 5.5 = 10.5, im = 7 — 2 = 5.
Запишем их рядом, добавив к мнимой части i: 10.5 + 5i
Полученное число и будет ответом: + =

Найти разность чисел и :
Найдём отдельно разности действительных частей и разности мнимых частей: re = 12 — 0 = 12, im = -1 — (-2) = 1.
Запишем их рядом, добавив к мнимой части i: 12 + 1i
Полученное число и будет ответом: — =

Найти произведение чисел и :
Найдём по формуле действительную и мнимую части: re = 2·5 — 3·(-7) = 31, im = 3·5 + 2·(-7) = 1.
Запишем их рядом, добавив к мнимой части i: 31 + 1i
Полученное число и будет ответом: * =

Найти отношение чисел и :
Найдём по формуле действительную и мнимую части: re = (75·3 — 50·4) / 25 = 1, im = (-50·3 — 75·4) / 25 = -18.
Запишем их рядом, добавив к мнимой части i: 1 — 18i
Полученное число и будет ответом: / =

Возведение комплексных чисел в степень

Начнем со всеми любимого квадрата.

Пример 9

Возвести в квадрат комплексное число

Здесь можно пойти двумя путями, первый способ это переписать степень как произведение множителей  и перемножить числа по правилу умножения многочленов.

Второй способ состоит в применении известной школьной формулы сокращенного умножения :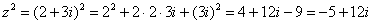

Для комплексного числа легко вывести свою формулу сокращенного умножения:. Аналогичную формулу можно вывести для квадрата разности, а также для куба суммы и куба разности. Но эти формулы более актуальны для задач комплексного анализа, поэтому на данном уроке я воздержусь от подробных выкладок.

Что делать, если комплексное число нужно возвести, скажем, в 5-ю, 10-ю или 100-ю степень? Ясно, что в алгебраической форме проделать такой трюк практически невозможно, действительно, подумайте, как вы будете решать пример вроде ?

И здесь на помощь приходит тригонометрическая форма комплексного числа и, так называемая, формула Муавра: Если комплексное число представлено в тригонометрической форме , то при его возведении в натуральную степень  справедлива формула:

Данная формула следует из правила умножения комплексных чисел, представленных в тригонометрической форме: чтобы найти произведение чисел ,  нужно перемножить их модули и сложить аргументы:

Аналогично для показательной формы: если , то:

Просто до безобразия.

Пример 10

Дано комплексное число , найти .

Что нужно сделать? Сначала нужно представить данное число в тригонометрической форме. Внимательные читатели заметили, что в Примере 8 мы это уже сделали:

Тогда, по формуле Муавра: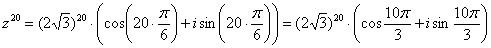

Упаси боже, не нужно считать на калькуляторе , а вот угол в большинстве случае следует упростить. Как упростить? Образно говоря, нужно избавиться от лишних оборотов. Один оборот составляет  радиан или 360 градусов. Выясним сколько у нас оборотов в аргументе . Для удобства делаем дробь правильной: , после чего становится хорошо видно, что можно убавить один оборот: . Надеюсь всем понятно, что  и  – это один и тот же угол.

Таким образом, окончательный ответ запишется так:

Любители стандартов везде и во всём могут переписать ответ в виде: (т.е. убавить еще один оборот и получить значение аргумента в стандартном виде).

Хотя  – ни в коем случае не ошибка.

Пример 11

Дано комплексное число , найти . Полученный аргумент (угол) упростить, результат представить в алгебраической форме.

Это пример для самостоятельного решения, полное решение и ответ в конце урока.

Отдельная разновидность задачи возведения в степень – это возведение в степень чисто мнимых чисел.

Пример 12

Возвести в степень комплексные числа , ,

Здесь тоже всё просто, главное, помнить знаменитое равенство.

Если мнимая единица возводится в четную степень, то техника решения такова:

Если мнимая единица возводится в нечетную степень, то «отщипываем» одно «и»,  получая четную степень:

Если есть минус (или любой действительный коэффициент), то его необходимо предварительно отделить: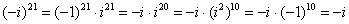

Пример 13

Возвести в степень комплексные числа ,

Это пример для самостоятельного решения.

Деление комплексных чисел

Давайте разделим (3+2i)/(1–4i)

В этот момент вы можете подумать, что можете просто разделить действительные и мнимые части… но не так быстро.

Как и в алгебре, мы должны разделить оба члена числителя на знаменатель, что оставляет нас с той же проблемой:

Что на
самом деле означает деление на комплексное число?

По правде говоря, это сбивает с толку. Разве не было бы хорошо, если бы мы могли избавиться от комплексного числа в знаменателе?

Хорошие
новости → Именно это мы и собираемся сделать!

Сопряжённые числа

Ключом к решению этой
проблемы является выяснение того, как преобразовать знаменатель в вещественное
число.

Самый простой способ
сделать это — использовать комплексное
сопряжение.

Комплексно-сопряжённое число какому-то числу это тоже самое число только с другим знаком возле мнимой части. И когда мы будем умножать комплексно-сопряжённые числа мы всегда будем получать действительное число.

Например, комплексно
сопряжённое число (1–4i) равно (1+4i).

Конечно, мы не можем просто умножить знаменатель на (1+4i). Как и с любой дробью, если мы умножаем знаменатель на значение, мы также должны умножить числитель на это значение

Теперь у нас есть произведение двух комплексных чисел в числителе дроби. С ними мы знаем как обращаться из предыдущего урока. А в знаменатели дроби получили 17, что означает уменьшение вектора в 17 раз.

Вы можете решить это с помощью графика или алгебраически:

Это было не так уж и сложно, не так ли?

Деление комплексных чисел

Как и при любом делении в алгебре, комплексное число нельзя делить на нуль
и на комплексное число .

При делении комплексного числа на действительное число на это число нужно
разделить и действительную, и мнимую компоненты. При делении комплексного числа на
комплексное число нужно делимое и делитель умножить на число, сопряжённое делителю.

Пример 9. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Автор проекта был свидетелем вопроса о том, откуда взялось 5 в знаменателе дроби.
Пояснения вызывают реакцию «А слона-то я и не заметил!». Пояснения следующие: не забываем, что мы
имеем дело с комплексными числами и знаем, что — это
не какая-нибудь переменная, а корень из минус единицы. Таким образом,

.

Пример 10. Разделить комплексное число
на комплексное число
.

Решение. Умножив числитель и знаменатель дроби
на , получаем:

Если всё же возникает вопрос, откуда в знаменателе дроби 10, смотрите пояснения в
конце предыдущего примера.

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

      Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

      Действительно, умножение и деление двух произвольных комплексных чисел  и  записанных в экспоненциальной форме, осуществляется по формулам

      Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

      При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

      Возведение комплексного числа   z = r e iφ в натуральную степень осуществляется по формуле

      Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Решение интегралов

Онлайн калькулятор предоставляет инструменты для интегрирования функций. Вычисления производятся как с неопределенными, так и с определенными интегралами. Ввод интегралов в поле калькулятора осуществляется вызовом групповой кнопки f(x) и далее:∫ f(x) — для неопределенного интеграла;b_a∫ f(x) — для определенного интеграла.

В определенном интеграле кроме самой функции необходимо задать нижний и верхний пределы.

Примеры вычислений интегралов:

$$\int \left(\frac{x^4}{x^3-6x^2+11x-6}\right)dx$$ (найти интеграл функции)

$$\int \left(\sqrt{x\sqrt{x\sqrt{x}}}\right)dx$$ (решить интеграл)

$$\int \left(\left(x^2+3x+5\right)\cos 2x\right)dx$$ (вычислить интеграл)

$$\int \left(\frac{x+\arccos ^2\left(3x\right)}{\sqrt{1-9x^2}}\right)dx$$ (решить интеграл)

$$\int _1^{e^3}\left(\frac{1}{x\sqrt{1+\log \left(x\right)}}\right)dx$$ (найти интеграл функции)

$$\int _{\frac{\pi }{6}}^{\frac{\pi }{3}}\left(\sin 6x\sin 7x\right)dx$$ (решить интеграл)

$$\int _{+\infty }^{-\infty }\left(\frac{1}{\left(x^2+1\right)\left(x^2+4\right)}\right)dx$$ (решить интеграл)

$$\int _1^2\left(x^2+\frac{1}{x}+\frac{1}{x^3}\right)dx$$ (вычислить интеграл)

Алгебраическая форма записи комплексных чисел

      Пусть x и y — произвольные вещественные числа.

      Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

      Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0).

      Комплексные числа, заданные парами (0, y), называют чисто мнимыми числами.

      Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.

      Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число   z, заданное парой вещественных чисел   (x, y), записывается в виде

z = x + i y .

(1)

где использован символ   i , называемый мнимой единицей.

      Число x называют вещественной (реальной) частью комплексного числа   z = x + i y   и обозначают   Re z.

      Число y называют мнимой частью комплексного числа   z = x + i y   и обозначают   Im z.

      Комплексные числа, у которых   Im z = 0 , являются вещественными числами.

      Комплексные числа, у которых     Re z = 0 , являются чисто мнимыми числами.

      Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Аргумент комплексного числа

      Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа   z.

      Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором    z.

      Аргумент комплексного числа  z  считают положительным, если поворот от положительного направления вещественной оси к  радиус-вектору z  происходит против часовой стрелки, и отрицательным  — в случае поворота по часовой стрелке (см. рис.).

      Считается, что комплексное число нуль аргумента не имеет.

      Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где  k  — произвольное целое число, то вводится, главное значение аргумента, обозначаемое   arg z   и удовлетворяющее неравенствам:

      Тогда оказывается справедливым равенство:

      Если для комплексного числа   z = x + i y   нам известны его модуль   r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам

(3)

      Если же комплексное число   z = x + i y   задано в алгебраической форме, т.е. нам известны числа   x   и   y,   то модуль этого числа, конечно же, определяется по формуле

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

      Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом  k  обозначать в Таблице 1 произвольное целое число.

      Таблица 1. – Формулы для определения аргумента числа   z = x + i y

Расположениечисла  z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественнаяполуось	x > 0 , y = 0	φ = 2kπ
	x > 0 , y > 0
Положительнаямнимаяполуось	x = 0 , y > 0
	x < 0 , y > 0
Отрицательнаявещественнаяполуось	x < 0 , y = 0	π	φ = π + 2kπ
	x < 0 , y < 0
Отрицательнаямнимаяполуось	x = 0 , y < 0
	x > 0 , y < 0

Расположениечисла  z	Положительнаявещественнаяполуось
Знаки x и y	x > 0 , y = 0
Главноезначениеаргумента
Аргумент	φ = 2kπ
Примеры

Расположениечисла  z
Знаки x и y	x > 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Положительнаямнимаяполуось
Знаки x и y	x = 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Отрицательнаявещественнаяполуось
Знаки x и y	x < 0 , y = 0
Главноезначениеаргумента	π
Аргумент	φ = π + 2kπ
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Отрицательнаямнимаяполуось
Знаки x и y	x = 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположение числа   z : Положительная вещественная полуось Знаки x и y : x > 0 ,   y = 0 Главное значение аргумента: Аргумент: φ = 2kπ Примеры:

Расположение числа   z : Знаки x и y : x > 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Положительная мнимая полуось Знаки x и y : x = 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Отрицательная вещественная полуось Знаки x и y : x < 0 ,   y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Отрицательная мнимая полуось Знаки x и y : x = 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Решение уравнений и неравенств

Математический калькулятор может решать уравнения и неравентства относительно переменной «x». Если есть необходимость найти другую переменную, например «y», то следует просто поменять их местами в выражении. Ввод переменных «x»,»y»,»z» производится в группе xyz нажатием соответствующих кнопок x, y, z.

Примеры решений уравнений и неравенств:

$$\frac{5}{12}+\frac{x}{6}=\frac{x}{4}+\frac{1}{3}$$ (решить уравнение)

$$x^2+12x+36=0$$ (решить уравнение)

$$\left(x+8\right)^2=x^2+8$$ (решить уравнение)

$$\left(x^2+\frac{1}{x^2}\right)+\left(x+\frac{1}{x}\right)=4$$ (решить уравнение)

$$\frac{19-x^2-4x}{49-x^2}(решить неравенство)
$$\frac{x}{3}+\frac{2x-1}{5}>2x-\frac{1}{15}$$ (решить неравенство)

$$\frac{\left(x-1\right)^2\left(x+7\right)\left(x+3\right)^3}{x^2+6x+9}\ge 0$$ (решить неравенство)

Формула Эйлера. Экспоненциальная форма записи комплексного числа

      В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера:

cos φ + i sin φ = e iφ .

(6)

      Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число   z = x + i y   может быть записано в виде

z = r e iφ ,

(7)

где   r   и   φ   — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству   r > 0 .

      Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа.

      Из формулы (7) вытекают, в частности, следующие равенства:

а из формул (4) и (6) следует, что модуль комплексного числа

cos φ + i sin φ,

или, что то же самое, числа   e iφ,   при любом значении   φ   равен 1.

Формы представления комплексных чисел

Комплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.

• Алгебраическая форма — наиболее часто используемая форма комплексного числа, запись числа в виде суммы действительной и мнимой частей: , где x — действительная часть, а y — мнимая часть
• Тригонометричкая форма — запись вида , где r — модуль комплексного числа (r = |z|), а φ — аргумент этого числа (φ = arg(z))
• Показательная форма — запись вида , где r — модуль комплексного числа (r = |z|), e — число Эйлера, а φ — аргумент комплексного числа (φ = arg(z))

Пример:

Переведите число 1+i в тригонометрическую и показательную формы:

Решение:

• Найдём радиус (модуль) комплексного числа r: r = √(12 + 12) = √2
• Найдём аргумент числа: φ = arctan(
  1
  1
  ) =
  π
  4
  = 45°
• Запишем результат в тригонометрической форме:
• Запишем результат в показательной форме:

Извлечение корня натуральной степени из комплексного числа

      Пусть — произвольное комплексное число, отличное от нуля.

      Корнем   n — ой степени из числа  z , где  называют такое комплексное число   z = r e iφ , которое является решением уравнения

z n = z .

(8)

      Для того, чтобы решить уравнение (8), перепишем его в виде

и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна   2kπ ,   где   k   — произвольное целое число. По этой причине справедливы равенства

следствием которых являются равенства

(9)

      Из формул (9) вытекает, что уравнение (8) имеет   n   различных корней

(10)

где

причем на комплексной плоскости концы радиус-векторов   z_k   при   k = 0 , … , n – 1   располагаются в вершинах правильного   n — угольника, вписанного в окружность радиуса  с центром в начале координат.

      Замечание. В случае   n = 2   уравнение (8) имеет два различных корня   z₁   и   z₂ , отличающихся знаком:

z₂ = – z₁ .

      Пример 1. Найти все корни уравнения

z3 = – 8i .

      Решение. Поскольку

то по формуле (10) получаем:

      Следовательно,

      Пример 2. Решить уравнение

z2 + 2z + 2 = 0 .

      Решение. Поскольку отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:

      Так как

то решения уравнения имеют вид

z₁ = – 1 + i ,       z₂ = – 1 – i .

Вычисление выражений с логарифмами

В калькуляторе кнопкой log_e(x) возможно задать натуральный логарифм, т.е логарифм с основанием «e»: log_e(x) — это ln(x). Для того чтобы ввести логарифм с другим основанием нужно преобразовать логарифм по следующей формуле: $$\log_a \left(b\right) = \frac{\log \left(b\right)}{\log \left(a\right)}$$ Например, $$\log_{3} \left(5x-1\right) = \frac{\log \left(5x-1\right)}{\log \left(3\right)}$$

Примеры решений выражений с логарифмами:

$$\log _3\left(5x-1\right)=2$$ преобразуем в $$\frac{\log \left(5x-1\right)}{\log \left(3\right)}=2$$ (решить уравнение)

$$\log _2\left(x\right)=2\log _x\left(2\right)-1$$ преобразуем в $$\frac{\log \left(x\right)}{\log \left(2\right)}=2\cdot \frac{\log \left(2\right)}{\log \left(x\right)}-1$$ (найти x в уравнении)

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Сопряженные числа и их свойства

Пусть —
комплексное число. Число ,
отличающееся от числа лишь знаком
при мнимой части, называется числом, сопряжённым с .

Свойства сопряжённых чисел

1) (число,
сопряжённое сопряжённому числу, равно данному числу);

2) если и —
комплексные числа, то и
(число, сопряжённое
с суммой двух чисел, равно сумме чисел, сопряжённых со слагаемыми и число, сопряжённое с
произведением, равно произведению чисел, сопряжённых с сомножителями).

3) если ,
то и
— положительное
действительное число, равное нулю тогда и только тогда, когда ,
т. е. когда и
.

Пример 8. Даны комплексные числа
и
. Убедиться
в справедливости свойств сопряжённых чисел.

Решение. Сопряжёнными данным комплексным числам являются числа
и . Сумма данных комплексных чисел:

,

а произведение:

.

В свою очередь

,

Таким образом, справедливость свойств сопряжённых чисел доказана.

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90

Ответ: единица

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60

Решение: 0,5

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав , появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой .

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем , либо для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой получится 230, а во втором, после нажатия и получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

Упрощение выражений, раскрытие скобок, разложение многочленов на множители

Калькулятор позволяет произвести некоторые алгебраические преобразования с выражениями. Результат выводится в нескольких вариантах упрощения/разложения/раскрытия скобок и пр.

Примеры:

$$x^4+x^2a^2+a^4$$ (разложить на множители)

$$\frac{6x^3-24x^2}{6x^3}$$ (разложить на множители)

$$(5x-2y^2)(5x+2y^2)$$ (раскрыть скобки)

$$(a-b)(a+b)(a^2+b^2)(a^4+b^4)(a^8+b^8)$$ (раскрыть скобки)

$$\frac{a^3-8}{a^2+2a+4}$$ (раскрыть скобки)

$$\frac{\left(\frac{2a}{2a+b}-\frac{4a^2}{4a^2+4ab+b^2}\right)}{\left(\frac{2a}{4a^2-b^2}+\frac{1}{b-2a}\right)}+\frac{8a^2}{2a+b}$$ (упростить выражение)

$$\frac{1-\sin ^4\left(x\right)-\cos ^4\left(x\right)}{2\sin ^4\left(x\right)}+1$$ (упростить выражение)

$$\left(\sqrt{a}-\frac{a}{\sqrt{a}+1}\right)\cdot \frac{a-1}{\sqrt{a}}$$ (упростить выражение)

Изображение комплексных чисел радиус-векторами координатной плоскости

      Рассмотрим плоскость с заданной на ней   Oxy   и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

      Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число   z = x + i y   радиус–вектором с координатами   (x , y).

      Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.

      При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Комплексные числа — тригонометрическая форма

Казалось бы, плоскость двухмерная, так как для описания произвольной точки нужны два числа. На самом же деле можно обойтись одним числом. Для этого используется тригонометрическая форма представления. То есть z = a+bi можно представить как z = ×(cosφ+i×sinφ), где:

• — модуль комплексного числа. Это расстояние от соответствующей точки до начала координат на плоскости. Например, модуль 2 + 1,5i = 2,5.
• φ (argz) — аргумент комплексного числа. Он находится измерением угла между осью абсцисс и прямой, соединяющей начало координат с точкой, отвечающей числу. Аргумент 2 + 1,5i = 36,8°.

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: = √(a²+b²). Данная формула справедлива для любых значений a и b.

Для нахождения аргумента (φ или argz) нужно воспользоваться следующими формулами:

• Если a>0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле argz = arctg(b/a).
• Если a<0, b>0 (2-я координатная четверть), то аргумент нужно находить по формуле argz = π+arctg(b/a).
• Если a<0, b<0 (3-я координатная четверть), то аргумент нужно находить по формуле argz = -π+arctg(b/a).

Как видно, комплексные числа не так сложны, как могло бы показаться на первый взгляд. Ознакомившись с простым объяснением и методикой работы с ними, вы научитесь складывать, вычитать, умножать и делить комплексные числа. Также вы сможете переводить комплексные числа из алгебраической формы в тригонометрическую.

Действия над комплексными числами

Онлайн калькулятор имеет функционал для работы с комплексными числами (операции сложения, вычитания, умножения, деления, возведения в степень и пр.). Комплексное число обзначается символом «i» и вводится с помощью групповой кнопки xyz и кнопки i

Примеры операций с комплексными числами:

$$\frac{\left(1+i\right)\left(3+i\right)}{3-i}-\frac{\left(1-i\right)\left(3-i\right)}{3+i}$$ (найти разность комплексных чисел)

$$\left(1-i\right)^3+\left(1+i\right)^3$$ (найти сумму комплексных чисел)

$$\left(-2+3i\right)\left(5+4i\right)$$ (найти произведение комплексных чисел)

$$\frac{-5-6i}{-6i}$$ (найти частное комплексных чисел)

$$\left(-2+2i\right)^9$$ (выполнить возведение комплексного числа в степень)

$$\frac{\left(-7-8i\right)i^7}{\left(4-5i\right)\left(-3+i\right)}-\frac{4+4i}{-2-5i}$$ (выполнить действия над комплексными числами)

Сложение и вычитание комплексных чисел

Сложение и вычитание комплексных чисел — это безусловно, самая простая и понятная операция. Сложение/вычитание действительных частей комплексного числа переводит точку вправо/влево на действительной оси, а сложение/вычитание мнимых частей комплексного числа переводит точку вверх/вниз на мнимой оси.

Арифметически это работает так же, как объединение одинаковых членов в алгебре.

Например, если мы вычтем 1 — 4i из 3 + 2i, мы просто находим разницу действительных 3 — 1 = 2 и мнимых 2i — (-4i ) = 2i + 4i = 6i частей.

Это то же самое, что построить точку 3 + 2i и перенести ее влево на 1 единицу и вверх на 4 единицы. Получившаяся точка — это итоговый результат: 2 + 6i.

Также можно представить точки комплексной плоскости как вектор (Вектор – отрезок соединяющий две точки для которого указано, какая из его граничных точек является началом, а какая концом). В нашем случаем началом будет начало координат (0,0), а концом сама точка. Теперь внесём знак минус под скобки, чтобы у нас было сложение:

(3 + 2i) + (-1 + 4i)

И затем построим два вектора.

Чтобы узнать результат сложения перенесём параллельно начало одного вектора в конец второго. Поскольку сложение является коммутативным, не имеет значения, каким образом мы их складываем. a+b=b+а (свойство коммутативности)

Это может показаться излишним, но вот в чем дело: понимание векторного представления сделает умножение и деление комплексных чисел намного проще.

Вычисление пределов функций

Предел функции задается последовательным нажатием групповой кнопки f(x) и функциональной кнопки lim.

Примеры решений пределов:

$$\lim _{x\to -12}\left(\frac{x^3+1728}{x^2+18x+72}\right)$$ (найти предел функции)

$$\lim _{x\to 0}\left(\left(1-2x^2\right)^{\cot ^2\left(x\right)}\right)$$ (найти предел функции)

$$\lim _{x\to -1}\left(\frac{2x^2-3x-5}{1+x}\right)$$ (решить предел функции)

$$\lim _{x\to 0}\left(\frac{e^{\sin \left(4x\right)}-e^{\sin x}}{\log \left(1+4x\right)}\right)$$ (вычислить предел функции)

$$\lim _{x\to \infty }\left(\sqrt{3x^2+\sqrt{x^4+4x^3}}-2x\right)$$ (вычислить предел)

$$\lim _{x\to 1}\left(\frac{\left(2x^2+3\right)^{3x}}{2x^2-4^{\left(x+1\right)}}\right)$$ (решить предел функции)