Работа с числами в python

Деление без остатка

Чтобы выполнить деление на цело в Python, можно воспользоваться целочисленным делением. В этом случае результатом будет целое число, без остатка. Целочисленное деление в Python обозначается двумя косыми чертами «//».

В отличие от других языков программирования Python позволяет результату целочисленного деления быть как целым (int), так и дробным (float) числом. В обоих случаях дробная часть отбрасывается и получается число с окончанием «.0».

Примеры нахождения целой части от деления:

print(5 // 2)
print(0 // 2)
print(1234 // 5.0)

2
0
246.0

В первых двух случаях деление осуществлялось между целыми числами. Поэтому в результате было получено целое число. В третьем примере одно из чисел вещественное. В этом случае в результате получаем так же вещественное число (типа float), после запятой у которого 0.

Стандартные функции арифметики в Python

Чтобы вычислить остаток от целочисленного деления в Python, не всегда необходимо загружать математическую библиотеку. Некоторые функции интегрированы.

Интегрированные функции	Их цель	Примеры
целое число (х)	Преобразует действительное число в целое, т. Е. Дробная часть «усекается».	интервал (5.3) >>> 5 интервал (5.6) >>> 5 интервал (5,987) >>> 5
круглый (х)	Выражение округляется до ближайшего целого числа.	круглый (5,4) >>> 5,0 круглый (5,7) >>> 6,0 круглый (5.5) >>> 6.0 круглый (5,987) >>> 6,0
круглый (х, п)	Используется для округления дробной части до n десятичных знаков	круглый (5.8776.2) >>> 5,88 круглый (5.9876.3) >>> 5,988
брюшной (х)	Найдите форму выражения	брюшной пресс (-7) >>> 7 брюшной пресс (7,8) >>> 7,8 абс (-66,55) >>> 66,55

Функции, для которых библиотека должна быть связана (сначала необходимо ввести из математического импорта *), показаны в следующей таблице.

Функции	Их цель
потолок (x)	Функция нужна для округления числа до большего целого числа («вверх»)
самолет (x)	Функция нужна для округления числа до наименьшего целого числа («вниз»)
квадрат (x)	Вычислить корень числа
регистр (х)	Требовалось найти логарифм. Если указать базу, расчет будет соответствующим.
а также	Возвращает основание натурального логарифма
грех (х)	Вычислить тригонометрические функции, где x в радианах
cos (x)
загар (х)
asin (х)
acos (x)
атан (х)
atan2 (х, у)	Найдите полярный угол точки, заданной x и y
градусы (x)	Требуется для преобразования угла из радиан в градусы
радианы (х)	Функция, необходимая для преобразования угла из градусов в радианы
пи	Печатает значение константы π

В качестве примера ниже приведен код, в котором используются математические операторы.

Результат отображается следующим образом.

В математическом модуле есть много других функций. Здесь перечислены наиболее распространенные.

Программа на Python с векторизацией и построением графиков

Вернемся к задаче, описывающей вертикальное положение \( y \) мяча после
подбрасывания. Предположим, что нас интересуют значения \( y \) в
каждую миллисекунду первой секунды полета. Это требует повторения
вычисления \( y = v_0 t — 0.5 g t^2 \) тысячу раз.

Также построим график зависимости \( y \) от \( t \) на отрезке
\( \). Построение такого графика на компьютере подразумевает
рисование прямых отрезков между точками кривой, поэтому нам
понадобится много точек, чтобы создать визуальный эффект гладкой
кривой. Тысячи точек, которые мы вычислим, нам будет достаточно для
этого.

Реализацию таких вычислений и построения графика может быть
реализовано следующим сценарием (ball_plot.py):

# -*- coding: utf-8 -*-

from numpy import linspace
import matplotlib.pyplot as plt

v0 = 5
g = 9.81
t = linspace(, 1, 1001)

y = v0*t - 0.5*g*t**2

plt.plot(t, y)
plt.xlabel(u't (с)')
plt.ylabel(u'y (м)')
plt.show()

def height(t):
	h =  v0*t - 0.5*g*t**2
	return h

h = lambda t: v0*t - 0.5*g*t**2

Замечание

В нашем сценарии для символьных аргументов мы использовали префикс
(например, ), чтобы указать, что
символы содержатся в кодировке UTF8.

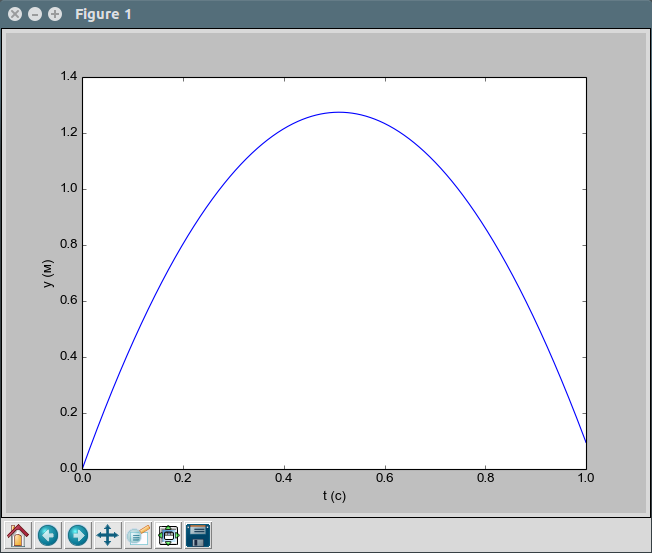
Данный сценарий строит график зависимости вертикального положения мяча
от времени (см. рис. :numref:`%s`). Отметим, что строки для
вычисления из сценария ball.py из раздела
мало изменены, но значение
вычисляется для тысячи точек.

Рассмотрим различия рассматриваемого сценария от предыдущих. Первое
отличие это строки, которые могли выглядеть следующим образом:

from numpy import *
from matplotlib.pyplot import *

Мы видим, что является модулем Python. Этот модуль содержит
огромный функционал для математических вычислений, а модуль
реализует возможности для построения двумерных
графиков. Приведенные выше строки представляют быстрый способ загрузки
всего функционала, связанного с вычислениями и построением
графиков. Однако, фактически мы используем только несколько функций в
нашем сценарии: , , и
. Многие разработчики считают, что мы должны импортировать
только то, что нам нужно, а не весь возможный функционал:

from numpy import linspace
from matplotlib.pyplot import plot, xlabel, ylabel

Другие предлагают способ импорта, когда используется префикс для
функций модуля

import numpy as np
import matplotlib.pyplot as plt

...

t = np.linspace(, 1, 1001)
   
...

plt.plot(x,y)

Мы будем использовать все три способа. В нашем сценарии мы
использовали два из них.

from numpy import linspace
import matplotlib.pyplot as plt

Рисунок 1: График, построенный с помощью нашего сценария.

Функция принимает три аргумента и, в общем случае,
вызывается следующим образом:

linspace(start, stop, n)

Функция генерирует равноотстоящих координат,
начинающихся со значения , и заканчивающихся
. Выражение создает 1001 координату
от 0 до 1 включительно. Математически это означает, что отрезок
\( \) разбивается на 1000 равных отрезков и значения координат
в этом случае вычисляются следующим образом: \( t_i = i/1000,\ i = 0, 1,
\ldots, 1000 \).

Функция возвращает объект класса ,
т.е. некоторый набор чисел (массив). При выполнении арифметических операций с
такими объектами, на самом деле эти операции осуществляются для каждого
элемента массива. В результате получается аналогичный массив из 1001
элемента, который сохраняется в переменную . Таким образом
также является массивом.

Такой подход вычисления нескольких чисел в одну строку называется
векторизацией. Этот способ очень удобен, так как сокращает не только
количество кода, но и время вычислений по сравнению с использованием
циклов или .

Команды для построения графиков достаточно просты:

1. означает построение графика зависимости от

2. помещает текст на оси .

3. помещает текст на оси .

Нахождение всех простых множителей числа

Если пользователь вводит число как 12, то на выходе должно быть 2, 2, 3, а если на входе 315 – выход должен быть «3 3 5 7». Программа должна вернуть все простые множители данного числа. Простые множители 330 – это 2, 3, 5 и 11. Следовательно, 11 является наиболее значимым простым множителем 330.

Например: 330 = 2 × 3 × 5 × 11.

Прежде чем писать программу на Python, давайте разберемся со следующими догадками.

1-я гипотеза – может быть хотя бы один простой множитель, который будет меньше √n в случае, если n не является простым числом.

Доказательство. Существуют два больших числа sqrt(n), их произведение также должно делить n, но оно будет превышать n, что противоречит нашему предположению. Таким образом, не может быть более одного простого множителя n, большего, чем sqrt(n).

Давайте посмотрим на следующий шаг, чтобы выполнить такую операцию.

 
p <= sqrt(n} or q <= sqrt(n) 

2-я гипотеза – может быть более 1 простого множителя n больше, чем sqrt(n).

Доказательство. Предположим, что есть два больших числа sqrt(n), тогда их произведение также должно делить n, но оно будет больше n, что противоречит нашему предположению. Таким образом, не может быть более одного простого множителя n, большего, чем sqrt(n).

Давайте посмотрим на следующий шаг, чтобы выполнить такую операцию.

Пример – программа Python для печати простых множителей.

 
import math 
# Below function will print the 
# all prime factor of given number 
def prime_factors(num): 
    # Using the while loop, we will print the number of two's that divide n 
    while num % 2 == 0: 
        print(2,) 
        num = num / 2 
 
    for i in range(3, int(math.sqrt(num)) + 1, 2): 
 
        # while i divides n , print i ad divide n 
        while num % i == 0: 
            print(i,) 
            num = num / i 
    if num > 2: 
        print(num) 
# calling function  
 
num = 200 
prime_factors(num) 

Выход:

2 
2 
2 
5 
5 

Объяснение –

В приведенном выше коде мы импортировали математический модуль. Функция prime_factor() отвечает за печать составного числа. Сначала мы получаем четные числа; после этого все оставшиеся простые множители должны быть нечетными. В цикле for число должно быть нечетным, поэтому мы увеличили i на два. Цикл for будет вычислять квадратный корень n раз.

Давайте разберемся в следующем свойстве составных чисел.

Каждое составное число имеет хотя бы один простой множитель, меньший или равный квадратному корню.

Программа будет работать следующим образом:

• На первом шаге найдем наименьший простой множитель i.
• Вхождение i будет удалено из n путем многократного деления n на i.
• Повторим оба вышеуказанных шага для деления n и i = i + 2. Оба шага будут повторяться до тех пор, пока n не станет либо 1, либо простым числом.

Давайте разберемся в другом примере, где мы находим наибольший простой множитель данного числа.

Пример – 2: Программа Python для определения наибольшего простого множителя заданного числа.

 
def largest_prime_factor(n): 
    i = 2 
    while i * i <= n: 
        if n % i: 
            i += 1 
        else: 
            n //= i 
    return n 
 
print(largest_prime_factor(345)) 

Выход:

23 

Изучаю Python вместе с вами, читаю, собираю и записываю информацию опытных программистов.

Остаток

Для получения остатка от деления в Python 3 используется операция, обозначающаяся символом процента «%». Остаток — это оставшаяся после целочисленного деления часть числа. Операция взятия остатка используется для решения различных видов задач.

Примеры:

print(10 % 3)
print(5 % 10)
print(5 % 0.25)

1
5
0.0

Определение остатка от деления очень часто используется в программах для нахождения, допустим, чётных чисел. Или, например, если обработка данных выполняется в цикле, и нужно выводить в консоль сообщение о ходе обработки не каждый раз, а на каждой 10-ой итерации.

Вот пример вывода чётных чисел из списка в консоль:

example_list = 
for value in example_list:
    if value % 2 == 0:
        print(value)

2
8
12

Операторы сравнения

Оператор
Пример
Смысл
Результат

Эквивалентно

если значение равно значению , в противном случае

Не эквивалентно

если не равно и в противном случае

Меньше

если меньше чем , в противном случае

Меньше или равно

если меньше или равно , в противном случае

Больше

если больше , в противном случае

Больше или равно

если больше или равно , в противном случае

Вот примеры используемых операторов сравнения:

>>> a = 10
>>> b = 20
>>> a == b
False
>>> a != b
True
>>> a <= b
True
>>> a >= b
False
>>> a = 30
>>> b = 30
>>> a == b
True
>>> a <= b
True
>>> a >= b
True

Операторы сравнения обычно используются в булевых контекстах, таких как условные операторы и операторы цикла, для процессом вычислений, как вы увидите позже.

Равенство для значений с плавающей точкой

Вспомните из более раннего обсуждения , что значение хранится внутри для объекта может быть не совсем таким, как вы думаете. По этой причине не рекомендуется сравнивать значения с плавающей точкой для точного равенства. Рассмотрим этот пример:

>>> x = 1.1 + 2.2
>>> x == 3.3
False

Бабах! Внутренние представления операндов сложения не совсем равны и , поэтому вы не можете полагаться на для точного сравнения с .

Предпочтительным способом определения того, являются ли два значения с плавающей точкой «равными», является вычисление того, находятся ли они близко друг к другу, с учетом некоторого допуска. Посмотрите на этот пример:

>>> tolerance = 0.00001
>>> x = 1.1 + 2.2
>>> abs(x - 3.3) < tolerance
True

Функция возвращает абсолютное значение. Если абсолютное значение разности между двумя числами меньше указанного допуска, они достаточно близки друг к другу, чтобы считаться равными.

Оператор деления

Деление в Python обозначается косой чертой «/». Примечательно, что результат в консоле всегда приводится к типу «float», даже если оба операнда были целочисленного типа, об этом свидетельствует появление «.0» у полученного значения.

Это появилось в 3-ей версии Python, ранее результатом деления целых чисел было только целое число, чтобы получить дробный результат, программисты явно указывали одному из операндов тип «float», в противном случае дробная часть просто отбрасывалась.

Важно понимать, что деление в Python, как и другие операции, работает медленнее, чем в более низкоуровневых языках программирования. Это связано с высоким уровнем автоматизации и абстракции, из-за динамической типизации интерпретатор вынужден приводить числа к дробному типу «float», который требует большего количества памяти

Деление в представлении человека отличается от его представления в компьютере. Компьютер устроен так, что все арифметические операции могут выполняться только через сложение. Это значит, что быстрее всего выполняется сложение, затем вычитание, где необходимо менять знак операндов, умножение, где число складывается много раз. Деление выполняется дольше всех, потому что помимо многократно повторяющейся операции сложения необходимо также менять знак операндов, что требует больше памяти и действий.

Примеры:

print(int(1) / int(2))
print(5 / 5)
print(1 / 3)

0.5
1.0
0.3333333333333333

Из примера видно, что не смотря на то, что во всех случаях операция была между целыми числами, результатом деления в Python 3 является вещественное число. В первом случае мы даже специально использовали приведение к типу int.

Дополнительно хотелось бы отметить, что если точности типа данных float не достаточно, можно воспользоваться библиотекой decimal. В частности мы её использовали при написании программы «калькулятор» в отдельной статье.

Побитовые операторы

Поразрядные операторы выполняют побитовую операцию со значениями двух операндов. Рассмотрим следующий пример.

Например,

 
if a = 7  
   b = 6    
then, binary(a) = 0111   
    binary(b) = 0110   
   
hence, a & b = 0011   
      a | b = 0111   
             a ^ b = 0100   
       ~ a = 1000 

Оператор	Описание
& (бинарный and)	Если оба бита в одном и том же месте в двух операндах равны 1, то 1 копируется в результат. В противном случае копируется 0.
| (бинарный or)	Результирующий бит будет равен 0, если оба бита равны нулю; в противном случае результирующий бит будет равен 1.
^ (бинарный xor)	Результирующий бит будет равен 1, если оба бита разные; в противном случае результирующий бит будет равен 0.
~ (отрицание)	Вычисляет отрицание каждого бита операнда, т. е., если бит равен 0, результирующий бит будет равен 1 и наоборот.
<< (сдвиг влево)	Значение левого операнда перемещается влево на количество битов, присутствующих в правом операнде.
>> (сдвиг вправо)	Левый операнд перемещается вправо на количество битов, присутствующих в правом операнде.

Арифметические Операторы

В следующей таблице перечислены арифметические операторы, поддерживаемые Python:

Оператор
Пример
Смысл
Результат

 (unary)

Положительное значение

Другими словами, он на самом деле ничего не делает. В основном это существует ради дополнения отрицательных значений.

 (binary)

Сложение
Сумма и

 (unary)

Отрицательное значение
Значение равно с обратным знаком

 (binary)

Вычитание

вычитается из

Умножение
Перемножение и

Деление
Частное от деления на . Результат всегда относится к типу .

Модуль
Остаток от деления на

Округляющее деление(также называется Целочисленное деление)
Частное от деления на , округлённое до ближайшего минимального целого

Степень
Возведение в степень

 
Вот несколько примеров использования этих операторов:

>>> a = 4
>>> b = 3
>>> +a
4
>>> -b
-3
>>> a + b
7
>>> a - b
1
>>> a * b
12
>>> a / b
1.3333333333333333
>>> a % b
1
>>> a ** b
64

Результатом обычного деления() всегда является значение типа , даже если операнды делится нацело:

>>> 10 / 5
2.0
>>> type(10 / 5)
<class 'float'>

Если результат деления по полу() положительный, то дробная часть как бы обрезается, оставляя только целую часть. Когда результат отрицательный, результат округляется до следующего наименьшего(большего отрицательного) целого числа:

>>> 10 / 4
2.5
>>> 10 // 4
2
>>> 10 // -4
-3
>>> -10 // 4
-3
>>> -10 // -4
2

Кстати, заметьте, что в сеансе REPL можно увидеть результат вычисления выражения просто набрав его после подсказки не испольуя оператор , точно так же можно увидеть знчение переменной:

>>> 25
25
>>> x = 4
>>> y = 6
>>> x
4
>>> y
6
>>> x * 25 + y
106

Целые числа и числа с плавающей запятой

Python имеет три встроенных числовых типа данных: целые числа, числа с плавающей запятой и комплексные числа. В этом разделе вы узнаете о целых числах и числах с плавающей запятой, которые являются двумя наиболее часто используемыми типами чисел. Вы узнаете о комплексных числах в следующем разделе.

Целые числа

Целое число – это целое число без десятичных знаков. Например, 1 – целое число, а 1.0 – нет. Имя для целочисленного типа данных – , которое вы можете увидеть с помощью :

Вы можете создать целое число, набрав желаемое число. Например, следующее присваивает переменной целое число 25:

Когда вы создаете такое целое число, значение 25 называется целочисленным литералом, потому что целое число буквально вводится в код.

Возможно, вы уже знакомы с тем, как преобразовать строку, содержащую целое число, в число с помощью . Например, следующее преобразует строку «25» в целое число 25:

не является целочисленным литералом, потому что целое значение создается из строки.

Когда вы пишете большие числа от руки, вы обычно группируете цифры в группы по три, разделенные запятой или десятичной точкой. Число 1000000 читать намного легче, чем число 1000000.

В Python нельзя использовать запятые для группировки цифр в целочисленных литералах, но можно использовать символы подчеркивания (_). Оба следующих способа являются допустимыми способами представления числа один миллион как целочисленного литерала:

Нет предела тому, насколько большим может быть целое число, что может быть удивительно, учитывая, что компьютеры имеют конечный объем памяти. Попробуйте ввести наибольшее число, которое вы можете придумать, в интерактивном окне IDLE. Python справится с этим без проблем!

Числа с плавающей запятой

Число с плавающей запятой(floating-point number) или сокращенно с плавающей запятой(float) – это число с десятичной запятой. 1.0 – это число с плавающей запятой, как и -2.75. Имя типа данных с плавающей запятой – float:

Как и целые числа, числа с плавающей запятой можно создавать из литералов с плавающей запятой(floating-point literals) или путем преобразования строки в число с плавающей запятой с помощью функции :

Есть три способа представить литерал с плавающей запятой. Каждое из следующих действий создает литерал с плавающей запятой со значением один миллион:

Первые два способа аналогичны двум методам создания целочисленных литералов. Третий подход использует нотацию E для создания литерала с плавающей запятой.

Чтобы написать литерал с плавающей запятой в нотации E, введите число, за которым следует буква e, а затем другое число. Python берет число слева от e и умножает его на 10, возведенное в степень числа после e. Итак, эквивалентно 1 × 10⁶.

Python также использует нотацию E для отображения больших чисел с плавающей запятой:

Число с плавающей запятой 200000000000000000.0 отображается как . Знак указывает, что показатель степени является положительным числом. Вы также можете использовать отрицательные числа в качестве показателя степени:

Литерал интерпретируется как в степени , что составляет 1/10000 или 0,0001.

В отличие от целых чисел, числа с плавающей запятой имеют максимальный размер. Максимальное число с плавающей запятой зависит от вашей системы, но что-то вроде должно выходить за рамки возможностей большинства машин. составляет 2 × 10⁴⁰⁰, что намного больше, чем общее количество атомов во Вселенной!

Когда вы достигнете максимального числа с плавающей запятой, Python вернет специальное значение с плавающей запятой, :

означает бесконечность, и это просто означает, что число, которое вы пытались создать, превышает максимальное значение с плавающей запятой, разрешенное на вашем компьютере. Тип по-прежнему :

Python также использует , что означает отрицательную бесконечность и представляет собой отрицательное число с плавающей запятой, которое превышает минимальное число с плавающей запятой, разрешенное на вашем компьютере:

Вы, вероятно, не будете часто сталкиваться с и как программист, если только вы не будете регулярно работать с очень большими числами.

Цикл while в Python

Цикл while в Python используется во многих программах. Он позволяет выполнять программу пока остается истинным условие. Приведем пример перебора числовой последовательности в заданном диапазоне. 

>>> number = 1           # присваиваем начальное значение переменной
>>> while number <= 7:   # запускаем цикл при условии значение number <=7
…     print(number)    # выводим значение number при каждом цикле
…     number += 1      # после каждого цикла увеличиваем значение на 1
…1
2
3
4
5
6
7

Вначале присваиваем значение переменной number. Затем запускаем цикл while до тех пор, пока значение переменной number не будет больше 7. При каждом проходе цикла выводим значение number и затем увеличиваем его на 1. Как только значение number станет больше 7 цикл прекращается. 

Получение матричного ввода от пользователя

До сих пор мы обсуждали предварительно определенные матрицы. Но что, если пользователь хочет ввести свои данные. Итак, разберем следующий пример пользовательской матрицы.

Пример –

 
# A example for matrix input from user  
row = int(input("Enter the number of rows:"))  
column = int(input("Enter the number of columns:"))  
 
# Initialize empty matrix  
matrix = []  
print("Enter the entries row wise:")  
 
# For user input  
for i in range(row):       # A outer for loop for row entries  
   a =[]  
   for j in range(column):     # A inner for loop for column entries  
      a.append(int(input()))  
   matrix.append(a)  
 
# For printing the matrix  
for i in range(row):  
   for j in range(column):  
      print(matrix, end = " ")  
   print()  

Выход:

Enter the number of rows:3 
Enter the number of columns:3 
Enter the entries row wise: 
5 
6 
7 
8 
9 
2 
4 
3 
1 
5 6 7  
8 9 2  
4 3 1 

Объяснение:

В приведенном выше коде мы взяли данные пользователя, чтобы ввести количество строк и столбцов. Мы ввели 3 строки и 3 столбца; это означает, что в матрице будет 9 элементов. В цикле for элементы вставляются в пустую матрицу с помощью функции append(). Второй цикл for используется для печати входных данных в матричном формате.

12 ответов

Лучший ответ

В Python 3.0 вернет , а вернет . Первая — это деление с плавающей запятой, а вторая — деление по полу, иногда также называемое целочисленным делением.

В Python 2.2 или более поздней версии в строке 2.x нет разницы для целых чисел, если вы не выполните , что заставляет Python 2.x принять поведение 3.0

Независимо от будущего импорта, вернет , так как это результат операции разделения по полу.

Подробное описание вы можете найти на

616

twasbrillig
13 Ноя 2014 в 08:33

Приведенные выше ответы являются хорошими. Я хочу добавить еще один момент. До некоторых значений оба они приводят к одному и тому же частному. После этого оператор деления на этаж () работает нормально, но не оператор деления ().

2

user207421
6 Июн 2019 в 04:37

Ответ уравнения округляется до следующего меньшего целого числа или с плавающей запятой с .0 в качестве десятичной точки.

2

G.Ant
3 Июн 2015 в 15:26

Результатом является , а не , поскольку тип возвращаемого значения возвращаемого значения из оператора соответствует правилам приведения в действие (приведение типа) в python ,

Python способствует преобразованию младшего типа данных (целое число) в более высокий тип данных (число с плавающей запятой), чтобы избежать потери данных.

-1

Lee Mac
9 Ноя 2018 в 22:55

реализует разделение по этажам независимо от вашего типа. Так даст , но оба , и дадут .

См. для подробностей

32

twasbrillig
13 Ноя 2014 в 08:24

Это помогает прояснить для строки Python 2.x, не является ни делением по полу, ни истинным делением. Текущий принятый ответ не ясен по этому вопросу. — это деление по полу, когда оба аргумента являются целыми, но это истинное деление, когда один или оба аргумента являются плавающими.

Вышесказанное говорит намного больше правды и намного яснее, чем второй абзац в принятом ответе.

65

ThinkingStiff
2 Мар 2013 в 19:41

• — это деление по полу, оно всегда даст вам минимальное значение результата.
• А другой является делением с плавающей точкой.

Ниже приведены различия между и ; Я выполнил эти арифметические операции в Python 3.7.2

1

Fatema T. Zuhora
17 Июл 2019 в 11:56

Как все уже ответили, это разделение по полу.

Почему это важно, так это то, что является однозначно разделенным по полу, во всех версиях Python от 2.2, включая версии Python 3.x. Поведение может меняться в зависимости от:

Поведение может меняться в зависимости от:

• Активный импорт или нет (локальный модуль)
• Параметр командной строки Python, или

21

u0b34a0f6ae
9 Ноя 2009 в 23:55

Python 2.7 и другие будущие версии python:

Отдел (/)

Делит левый операнд на правый операнд

Пример:

Отделение этажа (//)

Разделение операндов, где результатом является частное, в котором удаляются цифры после десятичной точки. Но если один из операндов отрицателен, результат получается беспорядочным, то есть округляется от нуля (в сторону отрицательной бесконечности):

Примеры: и , ,

Оба подразделения и оператор разделения этажа работают одинаково.

5

Cà phê đen
6 Июн 2019 в 06:33

Двойная косая черта, , делится на этаж:

4

ThinkingStiff
2 Мар 2013 в 19:35

— это деление по полу, оно всегда дает целое число результата. Другой — «регулярное» деление.

2

Adam Bellaire
8 Окт 2008 в 17:19

10

Jonas Sciangula Street
18 Мар 2014 в 18:23