Синусоида — свойства, формула и график функции

Строим график функции, заданный системой уравнений, в MS EXCEL

Построим в MS EXCEL график функции, заданный системой уравнений. Эта задача часто встречается в лабораторных работах и почему-то является «камнем преткновения» для многих учащихся.

Пусть дана система уравнений

Требуется на отрезке  построить график функции f(x). Параметры a = 5 и b = 2 необходимо задать в отдельных ячейках.

Решение (1 ряд данных)

Чтобы построить график функции в MS EXCEL можно использовать диаграмму типа График или Точечная.

СОВЕТ: О построении диаграмм см. статью Основы построения диаграмм в MS EXCEL. О различии диаграмм Точечная и График см. статью График vs Точечная диаграмма в MS EXCEL.

Создадим таблицу с исходными данными для x от -1 до 4, включая граничные значения (см. файл примера, лист Ряд1):

Шаг по х выберем равным 0,2, чтобы график содержал более 20 точек.

Чтобы построить диаграмму типа Точечная:

• выделите любую ячейку таблицы;
• во вкладке Вставка в группе Диаграммы выберите диаграмму Точечная с прямыми отрезками и маркерами.

Чтобы построить диаграмму типа График:

• выделите любую столбец f(x) вместе с заголовком;
• во вкладке Вставка в группе Диаграммы выберите диаграмму График маркерами.

У обеих диаграмм один общий недостаток — обе части графика соединены линией (в диапазоне х от 1 до 1,2). Из этого можно сделать ошибочный вывод, что, например, для х=1,1 значение функции равно около -15. Это, конечно же, не так. Кроме того, обе части графика одного цвета, что не удобно. Поэтому, построим график используя 2 ряда данных.

Решение (2 ряда данных)

Создадим другую таблицу с исходными данными в файле примера, лист График:

Второй и третий столбец таблицы будут использоваться для построения 2-х рядов данных. Первый столбец — для подписей по оси х. Для значений x>1 будет построен второй график (в степени 3/2), для остальных — парабола.

Значения #Н/Д (нет данных) использованы для удобства — в качестве исходных данных для ряда можно брать значения из целого столбца. В противном случае пришлось бы указывать диапазоны соответствующих ячеек при построении диаграммы.

При изменении шага по х — это вызвало бы необходимость перестроения диаграммы.

У такой диаграммы имеется недостаток — в диапазоне х от 1 до 1,2 на диаграмме теперь нет вообще значений. Чтобы избежать этого недостатка — построим диаграмму типа Точечная с 3-мя рядами данных.

Решение (3 ряда данных)

Для построения графика используем 2 таблицы с данными для каждого уравнения, см. файл примера, лист График.

Первое значение второго графика возьмем чуть больше 1, например, 1,00001, чтобы как можно ближе приблизиться к значению, в котором происходит разрыв двух графиков. Также для точки со значением х=1 построим на диаграмме одну точку (ряд №3), чтобы показать, что для этого х значение второго уравнения не вычисляется (хотя фактически вычисляется).

Особенности использования тригонометрических функций в Excel

Синтаксис функции SIN:

Синтаксис функции SINH:

Синтаксис функции COS:

Синтаксис функции COSH:

Каждая из приведенных выше функций принимает единственный аргумент число, который характеризует угол, заданный в радианах (для SIN и COS) или любое значение из диапазона вещественных чисел, для которого требуется определить гиперболические синус или косинус (для SINH и COSH соответственно).

1. Если в качестве аргумента любой из рассматриваемых функций были переданы текстовые данные, которые не могут быть преобразованы в числовое значение, результатом выполнения функций будет код ошибки #ЗНАЧ!. Например, функция =SIN(“1”) вернет результат 0,8415, поскольку Excel выполняет преобразование данных там, где это возможно.
2. В качестве аргументов рассматриваемых функций могут быть переданы логические значения ИСТИНА и ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно.
3. Все рассматриваемые функции могут быть использованы в качестве формул массива.

1. Синус гиперболический рассчитывается по формуле: sinh(x)=0,5*(ex-e-x).
2. Формула расчета косинуса гиперболического имеет вид: cosh(x)=0,5*( ex+e-x).
3. При расчетах синусов и косинусов углов с использованием формул SIN и COS необходимо использовать радианные меры углов. Если угол указан в градусах, для перевода в радианную меру угла можно использовать два способа:

• Функция РАДИАНЫ (например, =SIN(РАДИАНЫ(30)) вернет результат 0,5;
• Выражение ПИ()*угол_в_градусах/180.

Графики функций с модулем

Для качественного усвоения материала необходимо понимать, что такое модуль. Краткую информацию о нём можно найти на странице Математические формулы и таблицы в справочном материале Горячие формулы школьного курса математики.

Применение модуля тоже представляет собой геометрическое преобразование графика. Не буду создавать сверхподробный мануал, отмечу только те моменты, которые, с моей точки зрения, реально пригодятся для решения других задач по вышке.

Сначала посмотрим, что происходит, когда модуль применяется к АРГУМЕНТУ функции.

Правило: график функции  получается из графика функции  следующим образом: при  график функции  сохраняется, а при  «сохранённая часть» отображается симметрично относительно оси .

Пример 22

Построить график функции

И снова вечная картина: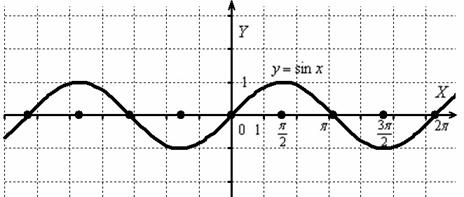
Согласно правилу, при  график сохраняется: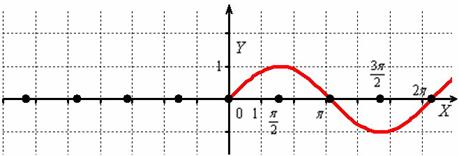
И сохранившаяся часть отображается симметрично относительно оси   в левую полуплоскость: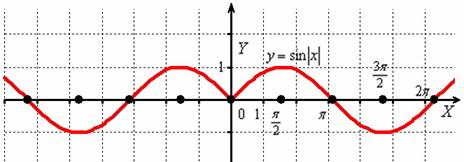

Действительно, функция  – чётная, и её график симметричен относительно оси ординат. Поясню детальнее смысл симметрии. Посмотрим на два противоположных значения аргумента, например, на  и . А какая разница? Модуль всё равно уничтожит знак «минус»: , то есть значения функции будут располагаться на одной высоте.

Функцию от модуля можно расписать в так называемом кусочном виде по следующему правилу: . В данном случае: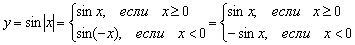

То есть, правая волна графика  задаётся функцией , а левая волна – функцией  (см. Пример 13).

Пример 23

Построить график функции

Аналогично, ветвь «обычной» экспоненты  правой полуплоскости отображаем симметрично относительно оси  в левую полуплоскость:
Распишем функцию в кусочном виде: , то есть правая ветвь задаётся графиком функции , а левая ветвь графиком .

Модуль не имеет смысл «навешивать» на аргумент чётной функции:  и т.п. (проанализируйте, почему).

И, наконец, завершим статью весёлой нотой – применим модуль к САМОЙ ФУНКЦИИ.

Правило: график функции  получается из графика функции  следующим образом: часть графика , лежащая НАД осью  сохраняется, а часть графика , лежащая ПОД осью  отображается симметрично относительно данной оси.

Странно, что широко известный график модуля «икс» оказался на 24-й позиции, но факт остаётся фактом =)

Пример 24

Построить график функции

Сначала начертим прямую, известную широкому кругу лиц: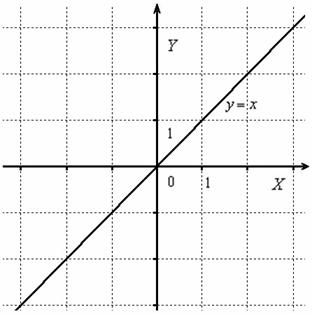
Часть графика, которая ВЫШЕ оси , остаётся неизменной, а часть графика, которая НИЖЕ оси  – отображается симметрично в верхнюю полуплоскость: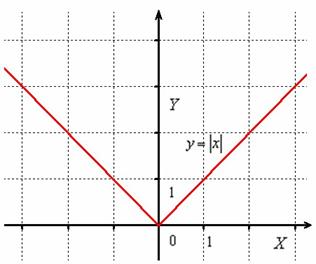

Модуль функции также раскрывается аналитически в кусочном виде:

Внимание! Формула отличается от формулы предыдущего пункта!

В данном случае: , действительно, правый луч задаётся уравнением , а левый луч – уравнением .

Кстати,  – редкий экземпляр, когда можно считать, что модуль применён, как к аргументу: , так и  к самой функции: . Изучим более «жизненную» ситуацию:

Пример 25

Построить график функции

Сначала изобразим график линейной функции :
То, что ВЫШЕ оси абсцисс – не трогаем, а то, что НИЖЕ – отобразим симметрично относительно оси  в верхнюю полуплоскость:

Согласно формуле , распишем функцию аналитически в кусочном виде: .

Или, упрощая оба этажа: , то есть правый луч задаётся функцией , а левый луч – функцией . Сомневающиеся могут взять несколько значений «икс», выполнить подстановку и свериться с графиком.

На какие функции модуль «не действует»? Модуль бессмысленно применять к неотрицательным функциям. Например: . Экспоненциальная функция и так полностью лежит в верхней полуплоскости: .

Всё возвращается на круги своя, синусом начали, синусом и закончим. Как в старой доброй сказке:

Пример 26

Построить график функции .

Изобразим сами знаете что =)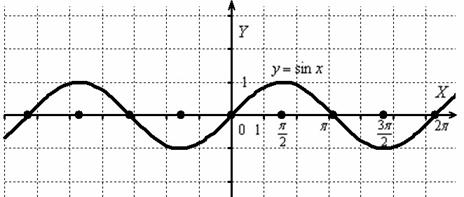

И снова – то, что находиться в верхней полуплоскости – оставим в покое, а содержимое подвала – отобразим симметрично относительно оси :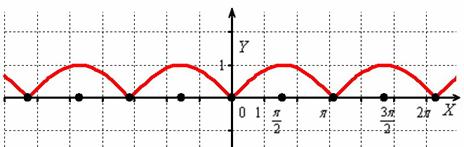

Кстати, понятен ли вам неформальный смысл такого симметричного отображения? Модуль «съедает» у  отрицательных чисел знак и делает их положительными, именно поэтому «подвальные» точки занимают противоположные места в верхней полуплоскости.

Распишем функцию в кусочном виде:

Решив два простейших школьных неравенства , получаем: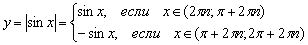, где  – любое целое число.

Да, статья была не самой приятной, но крайне необходимой. Однако повествование завершилось и стало немножко грустно =) Чем-то напомнило мне всё это урок про метод Симпсона, который тоже создавался в марте, и тоже достаточно долгое время. Наверное, громоздкие вещи пишутся по сезону =)

Желаю успехов!

(Переход на главную страницу)

Примеры использования функций SIN, SINH, COS и COSH в Excel

Пример 1. Путешественник движется вверх на гору с уклоном в 17°. Скорость движения постоянная и составляет 4 км/ч. Определить, на какой высоте относительно начальной точке отсчета он окажется спустя 3 часа.

Для решения используем формулу:

• B2*B3 – произведение скорости на время пути, результатом которого является пройденное расстояние (гипотенуза прямоугольного треугольника);
• SIN(РАДИАНЫ(B1)) – синус угла уклона, выраженного в радианах с помощью функции РАДИАНЫ.

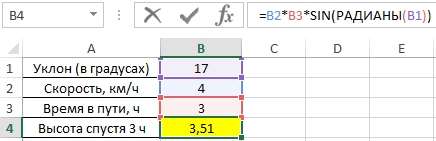
В результате расчетов мы получили величину малого катета прямоугольного треугольника, который характеризует высоту подъема путешественника.

Таблица синусов и косинусов в Excel

Пример 2. Ранее в учебных заведениях широко использовались справочники тригонометрических функций. Как можно создать свой простой справочник с помощью Excel для косинусов углов от 0 до 90?

Заполним столбцы значениями углов в градусах:

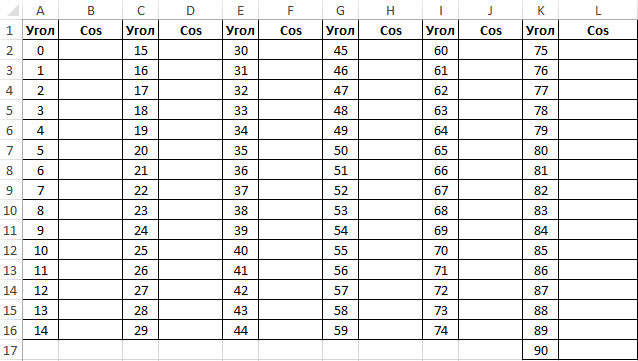
Для заполнения используем функцию COS как формулу массива. Пример заполнения первого столбца:

Вычислим значения для всех значений углов. Полученный результат:

Примечание: известно, что cos(90°)=0, однако функция РАДИАНЫ(90) определяет значение радианов угла с некоторой погрешностью, поэтому для угла 90° было получено отличное от нуля значение.

Аналогичным способом создадим таблицу синусов в Excel:

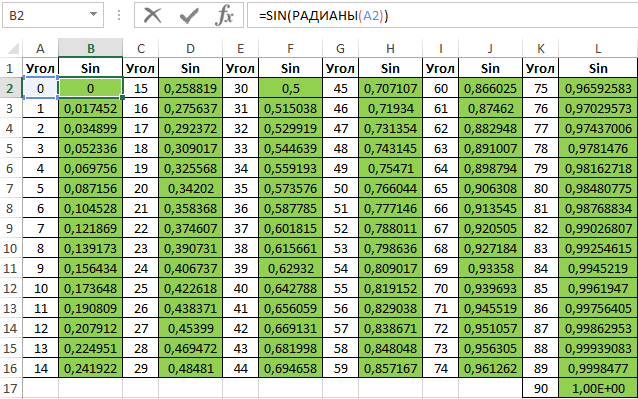
Значения основных функций тригонометрии

Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.

Определение 3

Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 . 

Определение 4

Тангенс по известному косинусу tg2α+1=1cos2α . 

Определение 5

Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α . 

Определение 6

Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 . 

Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере

Пример 6

Необходимо найти значение синуса угла π8, если tg π8=2-1 . 

Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1  Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеемsin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24

Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 .  sin π8=2-22.

π без картинок

Представьте себе слепого пришельца, который может различать только тени света и темноты. Можете ли вы объяснить ему, что такое π? Довольно сложно пояснить в такой ситуации понятие длины окружности, верно?

Давайте вернемся немного назад. Синус — это циклическая функция. Это означает, что значит ее значения должны…повторяться! Синус начинается с 0, идет к 1, к 0, к -1, к 0 и так далее.

Давайте определим π как время, за которое синус поднимается с 0 до 1, и обратно возвращается к 0. Вау! Теперь и мы используем π без всяких окружностей!

• Синус — это плавное передвижение вперёд-назад
• π — это время движения синуса с 0 до 1 и обратно до 0
• n * π (0 * π, 1 * π, 2 * π и т.д.) — это момент времени, в котором синус равен 0
• 2 * π, 4 * π, 6 * π и т.д. — полные периоды синуса.

Ага! Вот почему π встречается в таком количестве формул! π не «принадлежит» окружностям больше, чем 0 или 1 — π касается возвращения синуса в центр! Окружность — это пример фигуры, которая повторяется и возвращается в центр каждые 2*π единиц. Но вибрации, скачки и т.д. возвращаются к центру каждый π!

Вопрос: если π — это половина естественного периода, почему оно длится вечно (является иррациональным числом)?

Можно я отвечу вопросом на вопрос, А почему длина диагонали «единичной окружности» равна квадратному корню из 2, который также уходит в бесконечность?

Но да, я понимаю, что это философски не удобно, когда природа ведет себя произвольно. Но что поделаешь…

Насколько быстр синус?

Я вас немного запутал. Сначала я сказал: «представьте, что синусу нужно 10 секунд, чтобы добраться с 0 до максимума». А сейчас я говорю, что ему надо π секунд, чтобы добраться с 0 до максимума и обратно спуститься к 0. Что происходит?

• sin(x) — это базовая синусная волна, которой действительно требуется π единиц времени, чтобы пройти путь с 0 до максимума и опять до 0 (или 2*π, чтобы обойти свой полный период)
• sin(2x) — это синусоида, которая движется вдвое быстрее
• sin(x/2) — это синусоида, которая движется вдвое медленее базовой

Так что мы используем sin(n*x) , чтобы сделать синус, который будет двигаться так быстро, как нам нужно. Очень часто слово «синусоида» используется для указания общей формы волны, а не конкретной скорости.

Определение 2: Бесконечный ряд

Я спрятал слона в комнате: как мы вообще вычисляем синус? Мой калькулятор, что, каждый раз рисует окружность и замеряет его?

Рад вам поведать, как можно вычислить синус без окружностей.

Синус — это ускорение в сторону, противоположную тому, где вы находитесь.

Пользуясь нашим примером с банковским счётом: представьте, что ваш шеф каждую неделю решил менять вашу зарплату на сумму, противоположную текущей на вашем банковском счёте. Если у вас сейчас есть 50 рублей, на следующей неделе шеф выдаст на 50 рублей меньше. Конечно, поскольку ваш доход будет 75 рублей, вы всё еще будете в плюсе (75 — 50) но в итоге ваш баланс уменьшится, поскольку «прибавки» шефа превзойдут ваши доходы.

Но не отчаивайтесь! Как только баланс становится отрицательным (скажем, у вас -50 рублей), ваш босс выдаст вам на целых 50 рублей больше. Затем снова баланс станет отрицательным (с его ростом шеф выдает всё меньше денег), и так будет продолжаться постоянно. Баланс будет то положительный, то нулевой, то отрицательный.

Этот пример также поясняет, почему в нейтральной точке (в 0) скорость синуса максимальна: когда вы на максимуме, вы начинаете падать и собирать всё больше «отрицательных прибавок», которые довольно быстро тянут вас к 0. После прохождения 0 вы начинаете получать наиболее значительные положительные прибавки и замедляетесь., потому что как только уходите в плюс, шеф опять начинает отнимать от вашей зарплаты.

Между прочим: поскольку синус — это ускорение, обратное к вашему текущему положению, а окружность сделана из горизонтальной и вертикальной синусоиды… вы поняли! Круговое движение может быть описано как «постоянное движение в направлении, противоположном текущей позиции, по направлению к горизонтальному и вертикальному центру».

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически: – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте . – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Основные понятия

Кривая получается из синусоидальной дуги путём смещения к пи/2 в сторону со знаком минус. Кривая представляет график функции у=sin x. В формуле синусоиды y=a+b cos (cx+d) присутствуют следующие аргументы:

• a: показывает сдвиг графика синусоиды по оси Oy (чем больше значение, тем выше прямая);
• b: описывает растяжения функции по оси Oy (чем выше постоянная, тем сильнее колебания);
• c: определяет растяжение по оси Ох (если постоянная увеличивается, наступает период колебаний);
• d: описывает сдвиг по оси Ох (если d увеличивается, тогда при построении синусоиды учитывается сдвиг в область со знаком минус по оси абсцисс).

Тангенс угла

Синус и косинус являются основными, или, как говорят математики, прямыми тригонометрическими ф-циями. Однако есть ещё две производных тригонометрических ф-ций – тангенс и котангенс. Напомним, что тангенс угла в прямоугольном треугол-ке – это отношение противолежащего катета к прилежащему. Однако в тригонометрии куда удобнее пользоваться другим его определением. Тангенс – это отношение синуса угла к его косинусу:

Для получения тангенса на единичной окружности необходимо продолжить прямую, образующую угол α, до её пересечения с прямой х = 1. Точка их пересечения будет иметь координаты (1; tgα):

Заметим, что если α относится ко второй четверти, то тангенс получится отрицательным. Действительно, с одной стороны, соответствующая прямая пересечет линию х = 1 в точке, лежащей ниже оси Ох:

С другой стороны, мы знаем, что во второй четверти синус положителен, а косинус – отрицателен. Тогда их отношение, то есть тангенс, должно быть отрицательным:

Очевидно, что тангенс должен быть периодической ф-цией. Однако его период вдвое меньше 2π и составляет π. Действительно, углы, отличающиеся на π, будут иметь одинаковое значение тангенса, что видно из построения:

Это значит, что справедлива формула:

tg(α + π) = tg α

С другой стороны, это означает, что тангенсы углов из III четверти положительны, ведь они равны тангенсам углов из I четверти. Аналогично можно утверждать, что тангенсы углов из IV четверти отрицательны:

Также тангенс является нечетной ф-цией. Чтобы убедиться в этом, найдем с помощью единичной окружности tgα и tg (– α):

Из построения видно, что tg (– α) = tgα, поэтому тангенс попадает под определение нечетной ф-ции.

Доказать этот факт можно и иначе. Вспомним, что синус – это нечетная ф-ция, а косинус – четная. Тогда, используя определение тангенса, можно записать:

Для вычисления тангенса проще всего использовать его определение. Мы знаем синусы и косинусы стандартных углов, а потому, деля их друг на друга, сможем найти и тангенсы стандартных углов:

Ещё раз отметим, что важнее всего запомнить значения синусов и косинусов стандартных углов. Зная их, школьник всегда сможет самостоятельно вычислить тангенс.

Можно ли вычислить тангенс для угла π/2, то есть для 90°? Сделать это не получится, ведь cosπ/2 равен нулю. Если подставить cosπ/2 в формулу для вычисления тангенса, то получится деление на ноль! Так как тангенс – периодическая ф-ция, то его нельзя вычислить и в тех точках, которые отличаются от π/2 на целое число π.

В частности, тангенс не определен при х = – π/2.

Неизбежная окружность

У окружности есть синус. Да. Но увидеть синус внутри окружности — это всё равно, что получить из омлета яйца обратно, когда все они хорошенько друг с другом перемешаны!

Давайте помедленнее. В симуляторе установите такие параметры: vertical:none и horizontal: sine*. Видите, как смайлик движется вперёд-назад? Это и есть движение синуса. Небольшой фокус: обычно синус начинает свой цикл на нейтральной срединной точке и бежит к максимуму. На этот раз мы начинаем в максимуме и падаем к срединной точке. Синус, который «стартует на максимуме», называется косинусом, и это просто версия синуса (как горизонтальная прямая является версией вертикальной прямой)

Настало время для обеих синусных волн: установите параметры vertical:sine и horizontal:sine*. И… у нас получилась окружность!

Горизонтальные и вертикальные «прыжки» в сумме дали круговое движение. В большинстве учебников рисуют окружность и пытаются извлечь из нее синус, но я предпочитаю обратный подход: начать с простого горизонтального или вертикального движения и добавить противоположное.

Свойства и доказательства

К главным свойствам синусоиды относятся область значений (включая нуль) и определений, чётность/нечётность, периодичность, точки пересечения с осью координат, промежуточности постоянства, убывания и возрастания, минимум и максимум. При пересечении графика функции (ГФ) с осью Ох результат равняется нулю. Под значением синуса подразумевается ордината соответствующей точки единичной окружности.

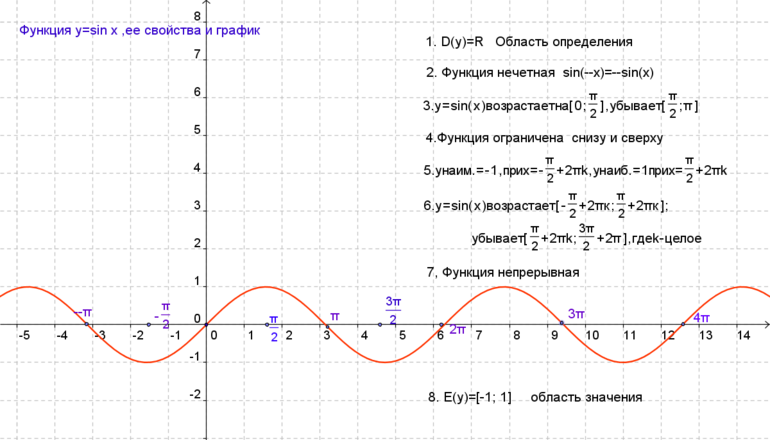
Значения ординаты единичной окружности (ЕД) расположены на отрезке . Они принимают значения от -1 до 1. Через любую точку указанного промежутка оси ординат, равного диаметром ЕД, проводится прямая, перпендикулярная оси ординат. Таким способом получается точка с рассматриваемой ординатой.

Из свойства вытекает следующее: функция y= sin x имеет область значений (-1; 1). Утверждение записывается так: E (sin x)=(-1; 1). Максимальное значение функции равняется единице. Подобное возможно, если соответствующей точкой ЕД является точка А. Минимальное число y равно -1 в случае, когда точкой ЕД является В (х=пи/2 +2пиk, где k принадлежит области Z.

Нечётность и постоянство

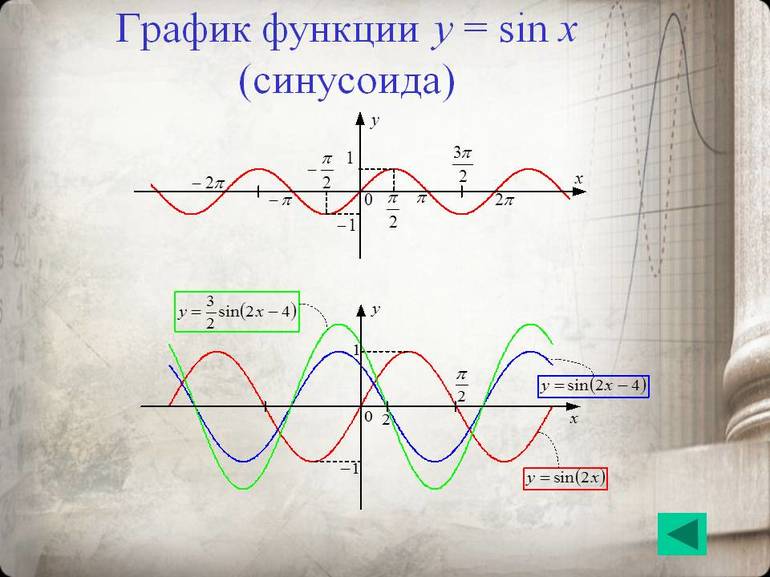
Функция считается нечётной, если sin (-x)=- sin x. Её график симметричен по отношению к началу координат. Сам синус является периодической величиной, у которой наименьший положительный период. Через отрезок 2пи вид кривой повторяется. Это свойство учитывается при построении графика.

Предварительно чертится кривая на любом отрезке соответствующей длины. При переносе линии влево и вправо соблюдается шаг в kT=2 πk, где k — любая натуральная цифра. Для вычисления точек пересечения линии с осями координат используется равенство х=0. Если значение подставить в функцию, получится следующее: y=sin 0=0. В таком случае график проходит через начало координат.

Так как y равен нулю, поэтому можно рассчитать х, воспользовавшись формулой y= sin x. Координата подходящей точки ЕД равняется нулю. Такое явление будет наблюдаться только в случае, если на ЕД будут выбраны точки D либо C, при x=πk, k принадлежит Z.

Функция имеет положительное значение в первой и во второй четвертях. На этих промежутках sin x больше нуля, а любое значение х находится в пределах 0-π. При решении задач учитывается период при всех x, принадлежащих отрезку (2πk; π+2πk), где k принадлежит Z. Функция считается отрицательной в третьем и четвёртом квадрате. При этом sin меньше нуля, а иск находится в пределах (пи+2пиk; 2пи+2пиk), k принадлежит области Z.

https://youtube.com/watch?v=bh1JvsyrdA8

Больше и меньше

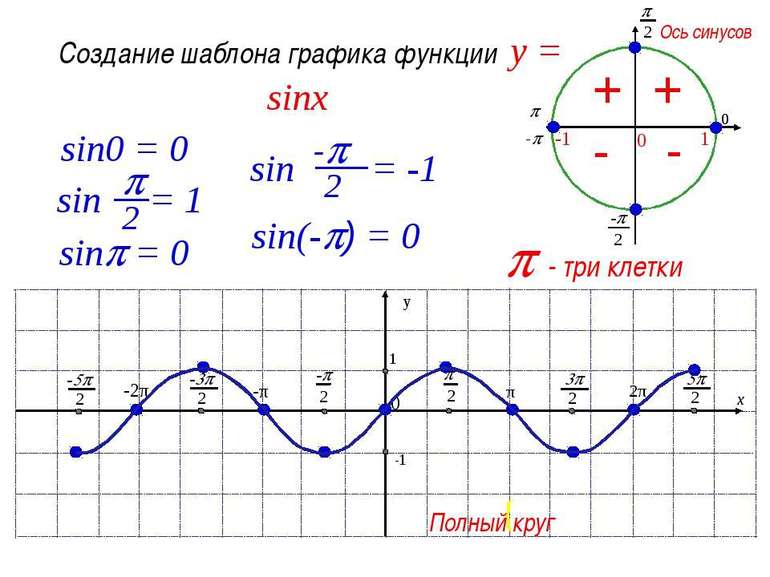
С учётом периодичности y с периодом T=2π исследуется функция на возрастание и убывание на любом отрезке длиной в 2пи. Если T= (-π/2;3π/2), а х принадлежит данному промежутку, тогда при увеличении аргумента изменится в большую сторону и ордината. Следовательно, на указанном отрезке синусоида возрастает.

Если учитывать её периодичность, можно прийти к выводу, что она возрастает на каждом интервале (-π/2+2πk; π/2+2πk), k принадлежит Z. Если х находится на отрезке (-π/2;3π/2), тогда при увеличении аргумента ордината ЕД уменьшается, а функция убывает. С учётом периодичности синусоиды можно сделать вывод, что она бывает на каждом отрезке (π/2+2πk;3π/2+2πk), k находится в области Z.

Основываясь на проведённом исследовании, строится график y=sin x. С учётом периодичности 2π предварительно строится график на любом отрезке соответствующей длины. Чтобы точно построить точки, рекомендуется придерживаться значения синуса (ордината ЕД). На основе нечётности проводится кривая, симметричная началу координат. При этом необходимо придерживаться интервала (-π;0). Так как линия строится на отрезке длиной 2π, поэтому учитывается периодичность величины.

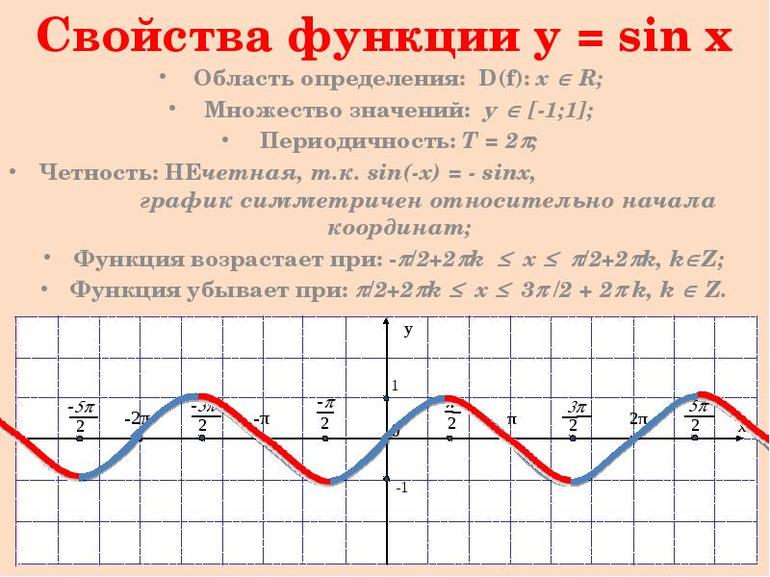
Вид графика повторяется на каждом отрезке с аналогичной длиной. Таким способом получается синусоида. Рассматриваемая тригонометрическая функция получила широкое применение в технике, физике и математике. Большинство процессов, включая колебания струн, напряжения в цепи, описываются с помощью функции, задаваемой формулой y= A sin (wx + f). Подобные явления считаются гармоническими колебаниями.

Кривая получается из синусоиды за счёт разных колебаний и путём параллельного переноса вдоль оси Ох. Чаще изменения результата связаны с функцией времени t. В таком случае используется формула y= A sin (wx + f), где через А обозначается амплитуда колебания, через w — частота, f — начальная фаза, 2пи/f — период колебания.

Варианты применения ИБП с аппроксимированной синусоидой

Как вы уже поняли, можно допускать применение инверторов ИБП: синусоидальная аппроксимация присутствует и с чистой синусоидой. Все зависит от оборудования, которое будет получать электроэнергию через такие источники.

Где ступенчатая синусоида не мешает

Если оборудование не имеет в своей схеме диммеров (электронных приборов регулировки), конденсаторов, индуктивных катушек и использует активную нагрузку, то оно не восприимчиво к той или иной синусоиде. Таких приборов не очень много, но они все-таки есть, и мы их широко используем в быту:

• обычные лампы накаливания;
• простые электроплиты;
• утюги, фены, паяльники;
• электрообогреватели типа каминов;
• электробойлеры (не все).

Негативное влияние аппроксимации

В Сети иногда проскакивает мнение, что все осветительные приборы могут функционировать от ИБП с аппроксимированной синусоидой, но это только полуправда. В большинстве случаев мы не используем не «лампочку Ильича», а более современные светильники с преобразователем напряжения ≈220-230 V. Подавляющее большинство людей даже не задумываются над принципами работы таких осветительных приборов, но посмотрите результаты теста некоторых из них, которые представлены в таблице ниже.

Отклонение от чистоты линии должно быть менее 8%Источник mykharkov.info

В таблице сравниваются параметры разных моделей светильников при подключении к обычной сети ≈220-230 V и к источнику бесперебойного питания, где присутствует ступенчатая аппроксимация синусоиды. Для эксперимента был использован ИБП компании APC с мощностью 500 V*A.

Даже неискушенный пользователь заметит, что электрические характеристики приборов освещения становятся другими при модифицированной синусоиде и эти изменения происходят с негативом – потребляемый ток возрастает, а КПД (яркость) падает. Возможна также ещё одна реакция, например, когда для ограничения мощности добавляют конденсатор, он соберет все реактивные токи, что одновременно будут делать диоды, и мощность, конечно же, увеличится в несколько раз, но это очень быстро выведет лампу из строя. Но при подключении к другому автономному ИБП 12/220 V такой картины не наблюдается, и лампа работает нормально.

Отсюда можно сделать вывод: подключение светодиодов или люминесцентных ламп на квази-синус зависит от случая: может сгореть, но может функционировать в нормальном режиме. Если говорить о правильной работе приборов, где в значительной степени присутствуют реактивные токи, а также для устройств, которые чувствительны к помехам, то придется использовать только источники типа on-line, выдающих чистую синусоиду.

Среди агрегатов, которым в любом случае противопоказана аппроксимированная синусоида можно назвать:

• все котлы отопления с электрическим циркуляционным насосом и электронным управлением;
• насосы для водоснабжения, в том числе гидрофоры и погружные модели;
• вентиляторы промышленного и бытового типа;
• вся техника с трансформаторами.

Чистый и модифицированный синус. В чем отличие.

Подводя итоги можно сказать, что использование ступенчатой синусоиды для приборов, генерирующих реактивные токи, в лучшем случае обернется невозможностью их запуска, а худшие варианты – это падение коэффициента мощности и даже быстрый выход из строя. Потому источники бесперебойного питания типа on-line, где на выходе чистый синус, это лучший вариант бесперебойника как на промышленном, так и на бытовом уровне. 

Как рисовать синусоиды в PowerPoint 2010

Если вам нужно нарисовать синусоиду в PowerPoint для презентаций, то здесь мы покажем различные подходы, которые можно использовать в зависимости от ваших потребностей.

Синусоида или синусоидальная волна представляет собой математическую кривую, которая описывает плавный повторяющиеся колебания. Она названа в честь функции синус, из которого она является граф.

Например, колебание незатухающой системы весенне-масс вокруг равновесия является синусоида может быть смоделирована с синусоидальной способом, или вы можете также смоделировать колебание маятника.

 Используйте Fooplot нарисовать идеальную кривую синусоида для PowerPoint

Как мы уже видели, Fooplot хороший онлайн инструмент, который позволяет создавать графики и сюжет какой-либо функции в Интернете. Мы можем указать грех и соз и сделать хорошую синусоиду для наших презентаций PowerPoint, а также другие математические графики для презентаций. Вы можете также использовать эту функцию, чтобы сделать шаблоны математические функции PowerPoint для загрузки.

После этого вы можете сгенерировать выходной файл как PNG или любой другой формат, и вставить его в PowerPoint 2010. Ниже вы можете увидеть пример PowerPoint слайд, показывающий функцию sin (х).

 Участок синусоидальной волны с помощью кривых Безье

Другой подход сделать этот вид кривых с помощью кривых Безье. Тем не менее, результат вы можете получить с помощью этих кривых не может быть совершенным. В зависимости от ваших потребностей презентации, вы можете выбрать между созданием синусоиде, используя этот подход или более точный подход, как построение синусоиду в Fooplot или Matlab.

Рисунок синусоидальной волны с помощью кривых Безье может быть не очень практичным на первый взгляд, и вам нужно отредактировать точки, чтобы сделать его более точным. Вы можете проследить в PowerPoint с помощью метода трассировки, что мы ниже объяснена над грехом (х) сюжет, созданный ранее как изображение. Тогда вы можете представить простую синусоиду волны, как в приведенном выше примере.

 Нарисуйте синусоиды в Excel и вставить его в PowerPoint

Другой подход должен был бы сделать синусоидальную кривую в Excel с помощью функции Excel греховную, а затем скопировать и вставить полученный рисунок в PowerPoint слайд. Используя этот подход.

Для построения синусоиды в Excel можно использовать инструкции в этом формате PDF. В основном то, что она предлагает, чтобы создать таблицу со следующей информацией: (.

Сек) Ввод частоты, Omega, амплитуда и Delta T.

Затем введите начальное время (в данном примере равен нулю) и заполнить колонку времени, используя уравнение авш Т + 1 = T + дельта. Теперь вы можете заполнить значения в рамках функции синусоида с помощью функции sin () в Excel.

Наконец, используйте XY график рассеяния для создания диаграммы.

Когда вы будете готовы, вы можете скопировать и вставить сюжет в презентации PowerPoint.