Алгебра

Поведение

Это нечетная функция, поскольку Ctg (-x) = — Ctg x. Таким образом, известно, что функция представляет собой симметрию относительно начала координат. Он также представляет уменьшение каждого интервала, расположенного между двумя последовательными вертикальными асимптотами.

Он не имеет максимальных или минимальных значений, потому что его приближения к вертикальным асимптотам представляют поведение, при котором функция увеличивается или уменьшается бесконечно.

Нули или корни функции котангенса находятся в нечетных кратных π / 2. Это означает, что Ctg x = 0 выполняется для значений вида x = nπ / 2 с n нечетным целым числом.

Некоторые функции в Excel

Функции предназначены для упрощения расчетов и имеют следующую форму: y=f(x), где y — результат вычисления функции, x — аргумент, f — функция.

Пример содержимого ячейки с функцией: =А5+sin(C7), где А5 — адрес ячейки, sin() — имя функции, в круглых скобках указывается аргумент, C7- аргумент (число, текст и т.д.), в данном случае ссылка на ячейку, содержащую число. Скобки — обязательная принадлежность функции, даже если у нее нет аргументов.

Excel содержит много функций, но прежде следует обратить внимание на следующие:

МАКС(список), например: МАКС(A1;A2;A3;…;An) — возвращает из списка максимальное число.

МИН(список), например: МИН(B1;B2;B3;…;Bn) — возвращает минимальное значение списка аргументов.

СРЗНАЧ(список) — возвращает среднее арифметическое своих аргументов.

ЦЕЛОЕ(Х) — округляет аргумент до ближайшего меньшего целого.

ОСТАТ(Число; Делитель) — возвращает остаток от деления.

СУММ(число1;число2;…) — возвращает сумму указанного списка, суммирует аргументы.

ABS(X) — возвращает модуль (абсолютную величину) числа

EXP(X) — возвращает экспоненту заданного числа.

LN(X) — возвращает натуральный логарифм заданного числа.

LOG10(X) — возвращает десятичный логарифм заданного числа.

LOG(X;a) — возвращает логарифм заданного числа X, по заданному основанию а.

SIN(X) — вычисляет синус угла Х, измеренного в радианах.

COS(X) — вычисляет косинус угла Х, измеренного в радианах.

TAN(X) — вычисляет тангенс угла Х, измеренного в радианах.

ASIN(X) — вычисляет арксинус угла Х в диапазоне от -pi/2 до +pi/2. pi=ПИ()=3,14159…

ACOS(X) — вычисляет арккосинус угла Х в диапазоне от 0 до pi.

ATAN(X) — вычисляет арктангенс угла Х в диапазоне от -pi/2 до +pi/2.

ГРАДУСЫ(угол) — преобразует радианы в градусы.

РАДИАНЫ(угол) — преобразует градусы в радианы.

СЕГОДНЯ() — возвращает текущую дату.

ГОД(дата) — возвращает, преобразует дату в год.

МЕСЯЦ(дата) — возвращает номер месяца.

ДЕНЬ(дата) — преобразует дату в день месяца.

Например, =СУММ(А1:А300) подсчитает сумму чисел в трехстах ячейках диапазона А1:А300 (напомним, что для указания диапазона ячеек между именами ячеек ставится двоеточие : , а для указания двух отдельных ячеек — точка с запятой ;).

Формат функции

ЕСЛИ (;;)

Первый аргумент функции ЕСЛИ( ) — логическое выражение, которое принимает одно из двух значений: «ИСТИНА» или «ЛОЖЬ». В первом случае функция ЕСЛИ() принимает значение , а во втором случае — значение .

В качестве или можно записать вложенную функцию ЕСЛИ( ). На месте логического выражения можно использовать одну из логических функций.

И( ) или ИЛИ( ).

Формат функций

И(;; …)

ИЛИ(;;…)

Функция И принимает значение ИСТИНА, если одновременно все логические выражения истинны. Функция ИЛИ принимает значение ИСТИНА, если хотя бы одно из логических выражений истинно.

Функция НЕ(A1) принимает значение ИСТИНА, если содержимое ячейки A1 равно 0, и ЛОЖЬ, если в A1 будет значение 1.

Для вставки функции в формулу можно воспользоваться «Мастером функций», вызываемым командой меню ВСТАВКА > ФУНКЦИЯ или специальной кнопкой fx.

Она относится к текстовым функциям Excel.
Она работает аналогично символу амперсанда (&) — сцепляет несколько значений в единую текстовую строку.
Например, формула
=СЦЕПИТЬ («До Нового года осталось «;ДАТА (2007;1;1)-СЕГОДНЯ (); « дней»)

вернет строку «До Нового года осталось 36 дней».

Тригонометрические функции в прямоугольном треугольнике

Чтобы определить тригонометрические функции произвольного угла возьмём произвольный прямоугольный треугольник, содержащий угол . Стороны этого треугольника мы будем называть так:

• Гипотенуза — сторона, противолежащая прямому углу, самая длинная сторона в треугольнике. В данном случае, сторона
• Противолежащий катет — катет, лежащий напротив угла. Например, катет — противолежащий по отношению к углу
• Прилежащий катет — катет, являющийся стороной угла. Например, катет — прилежащий по отношению к углу

Будем предполагать, что треугольник лежит в евклидовой плоскости, поэтому сумма его углов равна Это означает, что углы между катетами и гипотенузой лежат между и Используя формулы приведения или определение через единичную окружность, можно расширить область определения тригонометрических функций на множество вещественных чисел.

Си́нус угла — отношение противолежащего катета к гипотенузе: Это отношение не зависит от выбора треугольника , содержащего угол так как все такие треугольники подобны.

Ко́синус угла — отношение прилежащего катета к гипотенузе: Так как синус одного острого угла в треугольнике равна косинусу второго, и наоборот.

Та́нгенс угла — отношение противолежащего катета к прилежащему:

Кота́нгенс угла — отношение прилежащего катета к противолежащему: Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.

Се́канс угла — отношение гипотенузы к прилежащему катету:

Косе́канс угла — отношение гипотенузы к противолежащему катету:

Из определений тригонометрических функций следует:

и симметрично:

Использование функций в Excel 2007

Вы уже можете делать вычисления в Excel 2007, и уже использовали математическую функцию TAN, которая вычисляет тангенс. Кроме того, при выполнении сложения чисел Вы использовали функцию СУММ, которая вычисляет сумму ряда чисел.

В программе Excel встроено огромное количество других самых разнообразных функций. Функции в Excel используются и для вычислений, и для выполнения логических операций, и для операций с датами и текстом. По каждой функции в Excel есть справка, и Вы вполне можете самостоятельно узнать, как использовать ту или иную новую для Вас функцию.

Рассмотрим на практике использование некоторых функций Excel. Когда Вы выделяете ячейку, и затем нажимаете на fx перед строкой формул, по умолчанию Вам предложат функции Excel из категории 10 недавно использовавшихся функций. Но Вы можете в списке выбрать также следующие виды функций:

• полный алфавитный перечень
• финансовые
• дата и время
• математические
• статистические

и многие другие категории.

Давайте сначала рассмотрим математические функции Excel, как наиболее употребительные.

• ABS: возвращает модуль (положительное значение) числа. Поставьте в ячейку число -3, затем выделите другую ячейку, нажмите fx, выберите в категории математические функцию ABS, и вместо указания числа нажмите на ячейку с числом -3. В ячейке с функцией ABS появится значение 3.
• COS, SIN, TAN: возвращает значение косинуса, синуса, тангенса заданного числа, или значения заданной ячейки. Котангенса в функциях Excel нет, наверно, потому, что котангенс в формуле легко заменить единицей, деленной на тангенс.
• EXP: возвращает экспоненту заданного числа. Не знаете, что такое экспонента? Нажимаете на ссылку ниже: Справка по этой функции. Оказывается, экспонента — это число e (2,718…), возведенное в указанную степень. То есть экспонента числа -3 — это e в степени -3. Выделяете ячейку, выбираете EXP, и когда появится окошко с выбором числа, вместо числа указываете ячейку с числом.
• LN, LOG: возвращает значения натурального и десятичного логарифмов числа. Логарифмы вычисляются для положительных чисел, для числа -3 эти функции выдадут ошибку. Можно вычислить логарифм абсолютного значения (модуля) числа -3. Для этого выбираете функцию логарифма, и прямо в окошке для числа пишете ABS, ставите открывающую скобку, затем нажимаете на ячейку с числом -3, затем ставите закрывающую скобку. Нажимаете ОК. В ячейке появится значение логарифма, а в строке формул Excel — формула, например:=LN(ABS(B1)), где B1 — адрес ячейки с числом.
• LOG: требует уже два значения: само число и основание логарифма. Выберите эту функцию, и в окошки поставьте либо числа напрямую, либо ставите в окошки курсор, и выбираете ячейку с соответствующим числом. Адреса ячеек можно прописывать также и с клавиатуры, только следите, чтобы была английская раскладка клавиатуры.
• СУММ: можно суммировать отдельные числа, а можно целые диапазоны чисел: во втором случае достаточно при указании числа выделить соответствующий диапазон ячеек.

Функции в Excel могут быть не только математические. Хотите, например, узнать, сколько дней Вы прожили? Напишите в ячейку дату своего рождения в формате ДД.ММ.ГГГГ, например, 31.03.1971 (это мой день рождения). В другую ячейку вставьте функцию СЕГОДНЯ (она находится в категории Дата и время). В третью ячейку введите =, затем укажите ячейку с сегодняшней датой, затем поставьте — (минус), затем укажите ячейку с датой рождения. Получится что-то вроде:

=D2-D1, где D2 и D1 — адреса соответствующих ячеек.

И все, больше ничего не нужно делать. В ячейке будет количество дней между указанными датами, в данном случае, количество дней, которые Вы прожили.

Напоследок рассмотрим одну из логических функций ЕСЛИ. Простейший пример: введите в две ячейки какие-нибудь числа.

В третьей ячейке выберите функцию ЕСЛИ, в окошке Лог_выражение: выберите одну ячейку с числом, затем напишите =, выберите вторую ячейку.

В окошке Значение_если_истина: напишите слово равны, а в окошке Значение_если_ложь: напишите не равны. Нажмите ОК.

Если значения в ячейках не будут совпадать, функция ЕСЛИ выдаст «не равны», если будут, функция выдаст «равны».

Более подробные сведения Вы можете получить в разделах «Все курсы» и «Полезности», в которые можно перейти через верхнее меню сайта. В этих разделах статьи сгруппированы по тематикам в блоки, содержащие максимально развернутую (насколько это было возможно) информацию по различным темам.

Также Вы можете подписаться на блог, и узнавать о всех новых статьях. Это не займет много времени. Просто нажмите на ссылку ниже:

    Подписаться на блог: Дорога к Бизнесу за Компьютером

Арктангенс и арккотангенс − теория, примеры и решения

Функция арктангенс и ее график

Функция тангенс определена в интервале кроме точек , … и не является монотонной функцией (т.е. не является возрастающей или убывающей во всей области определения функции (Рис.1) (подробнее о функции тангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию тангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных отрезков функция tg x имеет обратную функцию. Отметим, что это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию обозначают x=arctg y. Поменяв местами x и y, получим:

Функция (1) − это функция, обратная к функции

График функции арктангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.2).

Свойства функции арктангенс.

1. Область определения функции: .
2. Область значений функции: .
3. Функция является нечетной: .
4. Функция возрастает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале для уравнения (2) существует одно t, для которого tg t=a. Это решение

Следовательно в интервале уравнение (2) имеет один корень. Так как тангенс периодичная функция с основным периодом π, то все корни уравнения (2) отличаются на πn (n∈Z), т.е.

Решение уравнения (2) представлен на Рис.3:

Так как tg t − это ординат точки пересечения прямой OM_t1 c прямым x=1, то для любого a на линии тангенса есть только одна точка T(1; a). Прямая OT_t пересекается с окружностью с радиусом 1 в двух точках: . Но только точка соответствует интервалу , которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

т.е.

Пример 2. Решить тригонометрическое уравнение:

Решение. Воспользуемся формулой (3):

Используя онлайн калькулятор получим:

Функция арккотангенс и ее график

Как известно, функция котангенс определена в интервале кроме точек -2π, —π 0, π, 2π,… и не является монотонной функцией (Рис.4) (подробнее о функции котангенс смотрите на странице Тангенс и котангенс. Онлайн калькулятор). А для того, чтобы функция имела обратную, она должна быть монотонной.

Однако, функцию кокотангенс можно разделить на интервалы, где она монотонна. Эти интервалы:

По теореме об обратной функции, на каждом из указанных интервалов функция ctg x имеет обратную функцию. Это различные обратные функции. Однако, предпочтение отдается обратной функции в отрезке . Обратную функцию оброзначают x=arcctg y. Поменяв местами x и y, получим:

Функция (4) − это функция, обратная к функции

График функции арккотангенс можно получить из графика функции с помощью преобразования симметрии относительно прямой y=x (Рис.5).

Свойства функции арккотангенс.

1. Область определения функции: .
2. Область значений функции: .
3. Функция не является ни четной ни нечетной (так как функция не симметрична ни относительно начала координит, ни относительно оси Y).
4. Функция убывает.
5. Функция непрерывна.

Решим тригонометрическое уравнение

В интервале (0; π) для уравнения (5) существует одно t, для которого сtg t=a. Это t=arcctg a. Следовательно в интервале (0; π) уравнение (5) имеет один корень. Так как котангенс периодичная функция с основным периодом π, то общее решение уравнения (5) имеет следующий вид:

Решения уравнения (5) можно представить на единичной окружности (Рис.6):

ctg t − это абсцис точки пересечения прямой с прямым y=1. Любому числу a на линии котангенс соответствует только одна точка . Прямая пересекется с единичной окружностью в двух точках . Но только точка соответствует интервалу (0; π), которое соответствует решению .

Пример 1. Решить тригонометрическое уравнение:

Решение. Воcпользуемся формулой (6):

Так как в интервале (0; π), то

Пример 2. Решить следующее тригонометрическое уравнение:

Решение. Используя формулу (6), имеем

С помощью онлайн калькулятора вычисляем . Тогда

Как рассчитывается?

Процедура разработки этих производных довольно проста. Все, что вам нужно сделать, это правильно определить аргумент и тип функции, которую он представляет.

Например, выражение Ctg (f / g) имеет деление в своем аргументе. Это потребует дифференциации относительно U / V после определения производной котангенса.

Котангенс — это величина, обратная касательной. Алгебраически это означает, что:

(1 / tg x) = ctg x

Ctg x = Cos x / Sen x

Неверно говорить, что функция котангенса является «обратной» касательной. Это потому, что функция арктангенса по определению является арктангенсом.

(Тг-1 x) = arctg x

Согласно тригонометрии Пифагора, котангенс участвует в следующих разделах:

Ctg x = (cos x) / (sin x)

Ctg2 x + 1 = Csc2 Икс

Согласно аналитической тригонометрии, он отвечает следующим тождествам:

Ctg (a + b) = (1 — tg a. Tg b) / (tg a + tg b)

Ctg (a — b) = (1 + tg a. Tg b) / (tg a — tg b)

Ctg (2a) = (1 — tg2 а) / (2тг а)

Ссылки

1. Тригонометрические ряды, Том 1. А. Зигмунд. Издательство Кембриджского университета, 2002 г.
2. Исчисление одной переменной. Рон Ларсон, Брюс Х. Эдвардс. Cengage Learning, 10 ноября 2008 г.
3. Исчисление с тригонометрией и аналитической геометрией. Джон Х. Саксон, Джон Саксон, Фрэнк Ван, Дайана Харви. Саксонские издательства, 1988 г.
4. Многопараметрический анализ. Сатиш Ширали, Харкришан Лал Васудева. Springer Science & Business Media, 13 декабря. 2010 г.
5. Системная динамика: моделирование, моделирование и управление мехатронными системами. Дин К. Карнопп, Дональд Л. Марголис, Рональд К. Розенберг. John Wiley & Sons, 7 марта 2012 г.
6. Исчисление: математика и моделирование. Уильям Баулдри, Джозеф Р. Фидлер, Фрэнк Р. Джордано, Эд Лоди, Рик Витрей. Эддисон Уэсли Лонгман, 1 января 1999 г.

История

Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.

Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.

Термины «тангенс» (от лат. «tangens» — касающийся) и «секанс» (лат. «secans» — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)

Как в Excel построить синусоиду

• Как построить график синусоиды в Excel.
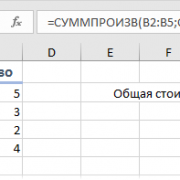
• Допустим имеется функция синусоиды, заданной уравнением y=sin4*x. Формула в Excel имеет вид:
• =SIN(4*C4)
• Требуется построить график функции.
• Функция в данном случае непрерывная, поэтому по оси x ограничим интервалом от 1 до -1, шаг возьмём 0,1.
• В итоги у нас должна получится таблица вида:

x	y=sin4*x
1	-0,75680
0,9	-0,44252
0,8	-0,05837
0,7	0,33499
0,6	0,67546
0,5	0,90930
0,4	0,99957
0,3	0,93204
0,2	0,71736
0,1	0,38942
	0,00000
-0,1	-0,38942
-0,2	-0,71736
-0,3	-0,93204
-0,4	-0,99957
-0,5	-0,90930
-0,6	-0,67546
-0,7	-0,33499
-0,8	0,05837
-0,9	0,44252
-1	0,75680

Переходим на вкладку Вставка -> Точечная с гладкими кривыми и маркерами.

Появится область графика, кликаем на белую область правым указателем мыши, выскакивает меню, далее Выбрать данные, появляется окно Выбора источника данных, выбираем весь диапазон данных нашей синусоиды в ячейках, затем Ок.

В итоги у нас получается график вида.

Также вид графика тоже можно настроить через конструктор и дополнительные инструменты.

Тангенс (tg x) и котангенс (ctg x) – свойства, графики, формулы

Справочные данные по тангенсу (tg x) и котангенсу (ctg x). Геометрическое определение, свойства, графики, формулы. Таблица тангенсов и котангенсов, производные, интегралы, разложения в ряды. Выражения через комплексные переменные. Связь с гиперболическими функциями.

Геометрическое определение ⇓Тангенс ⇓   График функции тангенс, y = tg x ⇓Котангенс ⇓   График функции котангенс, y = ctg x ⇓Свойства тангенса и котангенса ⇓   Периодичность ⇓   Четность ⇓   Области определения и значений, возрастание, убывание ⇓Формулы ⇓   Выражения через синус и косинус ⇓   Формулы тангенса и котангенс от суммы и разности ⇓   Произведение тангенсов ⇓   Формула суммы и разности тангенсов ⇓Таблица тангенсов и котангенсов ⇓Выражения через комплексные числа ⇓Выражения через гиперболические функции ⇓Производные ⇓Интегралы ⇓Разложения в ряды ⇓Обратные функции ⇓      Арктангенс, arctg ⇓      Арккотангенс, arcctg ⇓

См. также:

Синус, косинус — свойства, графики, формулы Обратные тригонометрические функции, их графики и формулы

|BD| –  длина дуги окружности с центром в точке A. α – угол, выраженный в радианах.

Тангенс (tg α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине прилежащего катета |AB|. Котангенс (ctg α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине противолежащего катета |BC|.

• ,    где n — целое.
• В западной литературе тангенс обозначается так: . Также приняты следующие обозначения:
• ;

; .

1. ,    где n — целое.
2. В западной литературе котангенс обозначается так: . Также приняты следующие обозначения:
3. ;

; .

Области определения и значений, возрастание, убывание

Функции тангенс и котангенс непрерывны на своей области определения (см. доказательство непрерывности). Основные свойства тангенса и котангенса представлены в таблице (n — целое).

y = tg x	y = ctg x
Область определения и непрерывность
Область значений	–∞	–∞
Возрастание	–
Убывание	–
Экстремумы	–	–
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	–

Производные

;     .

Производная n-го порядка по переменной x от функции : . Производная n-го порядка по переменной x от функции : . Вывод формул для тангенса > > >;     для котангенса > > >

Разложения в ряды

Чтобы получить разложение тангенса по степеням x, нужно взять несколько членов разложения в степенной ряд для функций sin x и cos x и разделить эти многочлены друг на друга,   . При этом получаются следующие формулы.

  при  .   при  . где Bn – числа Бернулли. Они определяются либо из рекуррентного соотношения: ; ; где   . Либо по формуле Лапласа:

Использованная литература: И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Г. Корн, Справочник по математике для научных работников и инженеров, 2012.

презентация потеме Функция тангенса, ее график и свойства. презентация к уроку по алгебре (10 класс) по теме

Слайд 1

Функция у = tg х и построение ее графика. .

Слайд 3

Определяем цели учебной деятельности 1.Выделите слова и словосочетания, встречаемые впервые. 2.Определите, знаете ли Вы точное значение этих слов, а также тех слов и словосочетаний, которые уже встречались Вам, но точные их значения и определения остаются Вам пока неизвестными.

Слайд 4

Определяем цели учебной деятельности 3 . Какие новые определения и значения каких понятий необходимо будет усвоить в рамках изучения данной темы? 4. Какие умения нужно будет выработать? 5. Какие правила, алгоритмы, способы действий Вам неизвестны , и для решения каких задач они Вам будут нужны?

• Слайд 5
• Тангенс.
• Слайд 6

Предполагаемые цели учебной деятельности учеников 1. Определение функции тангенса, свойств этой функции 2.Построение графика функции тангенс по таблице значений и тем свойствам, которые известны для тангенса (алгоритм построения). Узнать, н а какой линии находятся тангенсы углов.

Слайд 7

Находим ответы на вопросы в учебнике. Стр.17 -стр.18: определение , л иния тангенсов углов, о бласть определения, о бласть значений, с войства тангенса, известные вам на сегодняшний день.

1. Слайд 8
2. Рисунок 10 из учебника
3. Слайд 9

Функция у = tg х. Определение. Числовая функция, заданная формулой у = tg х , называется функцией тангенса. Тангенс угла – отношение ординаты точки на единичной окружности, соответствующей данному углу, к абсциссе этой точки. А где находятся тангенсы углов?

• Слайд 10
• Тригонометрический круг
• Слайд 11
• диктант a = 185 градусов a = – 185 градусов a = 102 a = – 102 a = 250 a = – 250 a = 375 a = 145 a = – 145 a = 225 a = – 315 a = 210 a = 590 a = – 15 1Углом какой четверти является угол a , если:
• Слайд 12

диктант 2. Вычислите : 1 вариант. cos 180 + 5sin 90 sin 180 – 3 cos 0 5ctg 90 – 7tg 180 sin 60 + cos 30 2 вариант. cos 0 + 3sin 90 sin 270 – 2cos 180 6tg 180 + 2ctg 90 1 + ctg 270 – 5 tg 360

Слайд 13

Нормы оценок 1.Все задания верны – оценка «5» 2. 1-2 ошибки – оценка «4» 3. 3- 5 ошибок – оценка «3» 4. более 5 ошибок – беру дополнительное домашнее задание. Успехов в учебе!

Слайд 14

Ответы к диктанту. 1вариант. 1. III,II,II,III,III,II,I. 2. 4,-3,0. 2 вариант. 1.II,III,III,I,III,III,IV. 2. 0,2,4. Задание . Заполнить в тетради таблицу значений для построения графика у = tg х. Работа в парах.

Слайд 15

Построение графика. Составляем план построения графика, пользуясь учебником.

Слайд 16

План построения графика. 1 . Правильно выбери единичный отрезок. 2. Н айди область определения. 3 Проведи прямые у = π/ 2 + π n , где n принадлежит целым числам. 4. Построй график. Работаем в парах.

1. Слайд 17
2. Линия тангенса
3. Слайд 18
4. График функции в 1 четверти у = tg x x y 0 1
5. Слайд 19
6. у = tg x х у y = tg x
7. Слайд 20

Выполнение заданий. №37(В),33(г). Устно составить план выполнения задания, обговорить в парах. Рефлексия. Ответьте на вопросы: Какие новые знания вы приобрели на этом уроке? Какие новые умения? Все ли цели урока были достигнуты? .

Слайд 21

Домашняя работа. 1. Построить по аналогичному график функции котангенс. 2.Уметь доказывать по рис 10 из учебника, что касательная к числовой окр ., проведенная в точке (1,0), является линией тангенсов.

36( а,б,в ),38(а), 39( а,в,г ) Творческое задание. По рис.11учебника, доказать, что касательная прямая, проведенная в точке (0,1) к числовой окружности, является линией котангесов . Спасибо за урок.

Слайд 22

Спасибо за урок.

Доказательство по определению производной

Следующее выражение соответствует производной по определению. Если расстояние между двумя точками функции приближается к нулю.

Подставляя котангенс, получаем:

Идентичности применяются для суммы аргументов и взаимности

Дробь в числителе традиционно оперируется

Исключая противоположные элементы и беря общий множитель, получаем

Применяя пифагорейские тождества и взаимность, мы должны

Элементы, вычисленные в x, являются постоянными по отношению к пределу, поэтому они могут оставить аргумент this. Затем применяются свойства тригонометрических пределов.

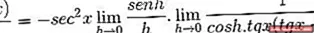
Лимит оценивается

Затем он факторизуется, пока не будет достигнуто желаемое значение.

Таким образом, производная котангенса противоположна квадрату косеканса.